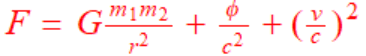PainterGuy said:
The end result given in the video is:
View attachment 275247
Such equation is essentially correct but let us deal with its standard form
\begin{equation*}
V(r) = \underbrace{\frac 1 2 \epsilon}_{\text{const.}} -\underbrace{\frac{GM}{r}\epsilon}_{\text{Newton}} +\underbrace{\frac{L^2}{2 r^2}}_{\text{Centripetal}} -\underbrace{\frac{GML^2}{r^3}\gamma}_{\text{Einstein}}
\end{equation*}
Where ##\epsilon## determines whether the particle orbiting the mass ##M## is massive or massless: if ##\epsilon = 1## then the particle is massive, if ##\epsilon = 0## then the particle is massless (note that the former implies that the observer follows a timelike path while the latter corresponds to an observer undergoing a null trajectory. As suggested by
@Ibix, you need to study further to fully understand the whole picture).
##\gamma=1## when relativistic effects are not negligible and ##\gamma=0## when Newtonian mechanics applies.
Studying the effective potential is useful to understand the types of trajectories (i.e. orbits) particles follow around massive objects.
I suggest not using software to plot the potential but sketching it yourself on a piece of paper.
In this particular problem you should study 4 cases:
- The trajectory followed by a massless particle by means of Newtonian mechanics.
- The trajectory followed by a massless particle by means of Einstein's relativity theory.
- The trajectory followed by a massive particle by means of Newtonian mechanics.
- The trajectory followed by a massive particle by means of Einstein's relativity theory.
Let us tackle 1.
Studying a massless particle (##\epsilon=0##) around a massive object under Newton's laws (##\gamma=0##) means having the potential reduced to
\begin{equation*}
V(r) = +\underbrace{\frac{L^2}{2 r^2}}_{\text{Centripetal}}
\end{equation*}
We are aimed at getting a conceptual understanding of the scenario, so we set ##L:=\sqrt{2}## (notice that the angular momentum of the system is conserved so we can always set it equal to a constant) and plot the effective potential
What is this plot telling us about the behaviour of light when a massive object is present?
Let's say a light ray is approaching ##M## straight from ##r=+\infty##. Notice that no matter with how much energy ##E=h \nu## light carries that there will always be a turning point, as the potential is unbounded and the energy of the incoming light-ray finite (i.e. ##E<V(r)##). Thus the light ray will get closer and closer to ##M## up to hitting the turning point (i.e. the point of closest approach). Once this happens, it will go straight to ##r=+\infty##.
Conclusion: light does not get bended.
Pictorially this means
If you want to prove that massless particles follow a straight line when GR effects are turned off, you will need to learn about the geodesic equation first.
I suggest you try 2., see what shape of the potential you end up getting and compare it to 1.
Hint: you should get a drastic difference.