- #1
Saitama
- 4,243
- 93
Homework Statement
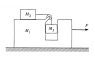
A "Pedagogical machine" is illustrated in the attachment. All surfaces are frictionless. What force F must be applied to ##M_1## to keep ##M_3## from rising or falling?
Ans. clue. For equal masses F=3Mg
Homework Equations
The Attempt at a Solution
I would like to do this problem in both inertial and non-inertial frames but first with the inertial frame.
The net force acting on the system is F. Hence,
[tex]F=(M_1+M_2+M_3)a \Rightarrow a=\frac{F}{M_1+M_2+M_3}[/tex]
Let a' be the acceleration ##M_2## and ##M_3## with respect to ##M_1##.
For ##M_1##, a normal force (at the point where it is in contact with ##M_3##) and a tension acts on it.
[tex]F-N-T=M_1a (*)[/tex]
For ##M_2##, ##T=M_2(a+a')##
For ##M_3##, ##M_3g-T=M_3a'## and ##N=M_3a##
Substituting T and N in the equation (*)
[tex]F=M_1a+M_3a+M_2a+M_2a'[/tex]
Solving, ##a'=0##. This is obviously wrong.
Any help is appreciated. Thanks!

 .
.