Solomon Chang
- 2
- 0
Hello everyone, I am reading Principia Lemma 10 and I cannot understand it. Can someone please help explaining? Thank you very much.
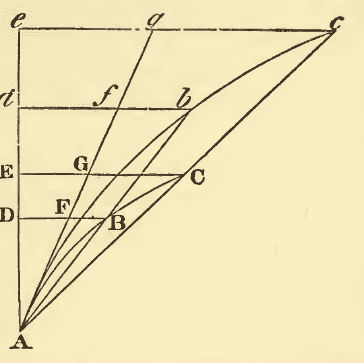


Furthermore, is there any way of understanding the Principia in a more numerical ways rather than words like this? Just asking.
Again, thank you very much.
Furthermore, is there any way of understanding the Principia in a more numerical ways rather than words like this? Just asking.
Again, thank you very much.