Monster007
- 26
- 1
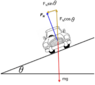
If a car us on a frictionless banked track what causes the normal reaction force to be greater than the weight force?
My understanding from what I've read is that the vertical component of the reaction force cancels the weight force which makes sense as the object doesn't leave the ground. And I understand that the horizontal component of the normal force (parallel to the plane) acts down the plane and provides the centripetal acceleration for the car to continue around the track. The question I have is, what is it that causes the normal to have this extra magnitude? I have read many different answers for this and by and large it is ignored in most explanations but I would love to get my head around this to properly understand the situation. Many thanks in advance.
My understanding from what I've read is that the vertical component of the reaction force cancels the weight force which makes sense as the object doesn't leave the ground. And I understand that the horizontal component of the normal force (parallel to the plane) acts down the plane and provides the centripetal acceleration for the car to continue around the track. The question I have is, what is it that causes the normal to have this extra magnitude? I have read many different answers for this and by and large it is ignored in most explanations but I would love to get my head around this to properly understand the situation. Many thanks in advance.