- #1
TylerH
- 729
- 0
Notation "(v*gradient operator)v" in Navier-Stokes
What does [itex]\left( \textbf{v} \cdot \nabla \right) \textbf{v}[/itex] mean, assuming knowledge of the gradient operator? And, specifically, how would that be expanded? In general, I'm ignorant of the notation [itex]\left( f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) y \right)[/itex] where, for example, [itex]f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right)[/itex] could be [itex]y + \frac{d}{dx}[/itex].
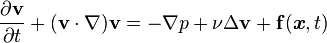
What does [itex]\left( \textbf{v} \cdot \nabla \right) \textbf{v}[/itex] mean, assuming knowledge of the gradient operator? And, specifically, how would that be expanded? In general, I'm ignorant of the notation [itex]\left( f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right) y \right)[/itex] where, for example, [itex]f \left( y, \frac{d}{dx}, \frac{d^2}{dx^2}, \ldots \right)[/itex] could be [itex]y + \frac{d}{dx}[/itex].