Deriving Navier-Stokes Equation

[Apashanka]

Just trying to derive the Navier-Stokes equation.
(1)The velocity at any point in space of an infinitesimal fluid element is v(x,y,z,t)
(2) acceleration $\frac{dv}{dt}=\frac{\partial v}{\partial t}+\sum_i\frac{\partial v_i}{\partial x_i}{\dot x_i}$
$a=\frac{dv}{dt}=\frac{\partial v}{\partial t}+\sum_i\frac{\partial v_i}{\partial x_i}{v_i}=\frac{\partial v}{\partial t}+(v • \nabla)v=\frac{Dv}{Dt}$
On the Rhs
(1) g acceleration due to gravity.
(2) acceleration due to pressure gradient (due to normal force on the surface)=$-\frac{\nabla p}{\rho}$
Therefore $\frac{Dv}{Dt}=g-\frac{\nabla p}{\rho}$+acceleration due to the tangential forces on the infinitesimal fluid element
Can anyone please help me out in how to calculate the acceleration due to tangential forces on the surface??
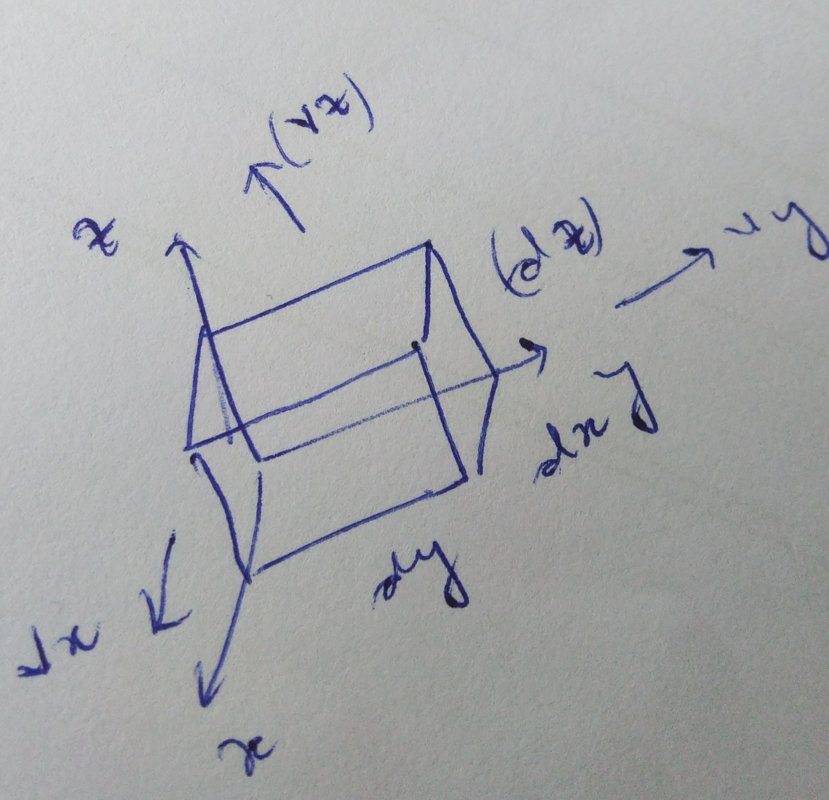
For the cubical infinitesimal volume element having edges dx,dy,dz
$F_x=\eta \frac{dv_x}{dz}|_{x,y}dxdy$
$F_y=\eta \frac{dv_y}{dz}|_{x,y}dx dy$
$F_z=\eta \frac{dv_z}{dy}|_{x,z}dx dz$
$a_x=\frac{\eta \frac{dv_x}{dz}|_{x,y}}{\rho dz}$
$a_y=\frac{\eta \frac{dv_y}{dz}|_{x,y}}{\rho dz}$
$a_z=\frac{\eta \frac{dv_z}{dy}|_{x,z}}{\rho dy}$
$\eta$ is the coefficient of viscocity
Can anyone please help me in how to proceed further to put these terms in the RHS of the navier Stokes equation??
Here is a rough diagram

 

[Chestermiller]

What is the relationship between the 6 components of the stress tensor and the components of the velocity gradient tensor for a viscous Newtonian fluid?

In your differential force balance equation, you omitted the term representing the divergence of the viscous stress tensor. Why?

 

[Apashanka]

What is the relationship between the 6 components of the stress tensor and the components of the velocity gradient tensor for a viscous Newtonian fluid?

The stress tensor components are $\sigma_{ij}=\frac{1}{2}(\frac{\partial v^i}{\partial x^j}+\frac{\partial v^j}{\partial x^i})$ and from Newton's law of viscocity the shear stress $\tau=\eta \frac{\partial v}{\partial x}$ that's what I have used...
But what will be the actual result and how it is coming will you please suggest...is my approach wrong??
I want to just do it with a very simplectic approach...

 

[Chestermiller]

The stress tensor components are $\sigma_{ij}=\frac{1}{2}(\frac{\partial v^i}{\partial x^j}+\frac{\partial v^j}{\partial x^i})$ and from Newton's law of viscocity the shear stress $\tau=\eta \frac{\partial v}{\partial x}$ that's what I have used...

This equation $\tau=\eta \frac{\partial v}{\partial x}$ is the one dimensional version of this equation $\sigma_{ij}=\frac{\eta}{2}(\frac{\partial v^i}{\partial x^j}+\frac{\partial v^j}{\partial x^i})$. You need to use the 3D version in deriving the NS equation.

But what will be the actual result and how it is coming will you please suggest...is my approach wrong??
I want to just do it with a very simplectic approach...

You can't do it with the simplistic approach because it is 3D. Also, in your approach, you omitted the changes in the stresses from one side of the cube to the other. The missing terms in your force balance are, for the x component, $$\frac{\partial \sigma_{xx}}{\partial x}+\frac{\partial \sigma_{xy}}{\partial y}+\frac{\partial \sigma_{xz}}{\partial z}$$

 

[Apashanka]

Okk using $\sigma_{ij}=\frac{\mu}{2}(\partial_j v^i+\partial_i v^j)$ the Rhs comes as $\frac{\mu}{2\rho}(\nabla^2 v)+\frac{1}{2\rho}(\nabla(\nabla • v))-\frac{\nabla p}{\rho}+g=\frac{Dv}{Dt}$