Oblique impact of smooth spheres?

AI Thread Summary
A sphere of mass m collides obliquely with a stationary sphere of mass M, with a coefficient of restitution e. The discussion centers on demonstrating that if m equals eM, the resulting motion directions after impact will be perpendicular. Participants suggest using vector representations and conservation of momentum to analyze the collision dynamics. One user shares a link to a helpful article that clarifies the concepts involved. The conversation emphasizes the importance of understanding the relationship between mass, velocity, and the coefficient of restitution in collision scenarios.
haddow64
Messages
14
Reaction score
0
1. A sphere of mass m impinges obliquely on a sphere of mass M, which is at rest. The coefficient of restitution between the spheres is e. Show that if m=eM, the directions of motion after impact are at right angles



2. Coefficient of restitution -
442cb57fc9daffed79a534632d0a5aad.png




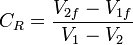
3. I really don't think I have a clue with this one, so far I have taken e and substituted it into m=eM to give

m = M x V_{}2f-V_{}1f/V_{}1

Can anyone give me any clues as to where to go next or am I going completely wrong with what I have?

Thanks in advance for any help
 
Physics news on Phys.org
Have you tried to draw a vector representation of your problem? Try this and make use of the conservation of momentum.
 
dlgoff said:
Have you tried to draw a vector representation of your problem? Try this and make use of the conservation of momentum.

This is what I have for the problem,

http://img156.imageshack.us/img156/2310/questioncb9.jpg

Do I have the right idea of what the collision looks like?

And how would I use the momentum conservation here, as in U1 (speed of m before) = V2 (speed of M after)?
 
Last edited by a moderator:
Well, that's not exactly what I had in mind.

Could you read over this http://instruct.tri-c.edu/fgram/web/elastic.htm" and let me know if it helps?
 
Last edited by a moderator:
Ah, that article was exactly what I needed, thanks for your help :D
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Coefficient of Restitution for a Hypothetical Collision where masses are not equal after the collision compared to before the collision
Replies
6
Views
1K
Test question: What is true for a mechanical impact?
Replies
7
Views
1K
Impact and collision - having problems
Replies
12
Views
2K
Oblique Impact of Smooth Spheres
Replies
2
Views
3K
Oblique collision with two spheres one of which is at rest
Replies
2
Views
3K
Complex collision with masses and Velcro
Replies
4
Views
2K
Oblique collision involving two spheres
Replies
8
Views
4K
MIT OCW 8.01 PS11.3: Elastic Collision Between Ball and Pivoted Rod
Replies
10
Views
2K
Sphere striking an incline (not asking for solutions....)
Replies
3
Views
1K
Newton's shell theorem - all mass is concentrated at its centre
Replies
16
Views
1K

Hot Threads

Recent Insights

Back
Top