On the width of the kinetic energy distribution of a gas

[Aaron121]

In these lecture notes about statistical mechanics, page $10$, we can see the graph below.

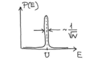
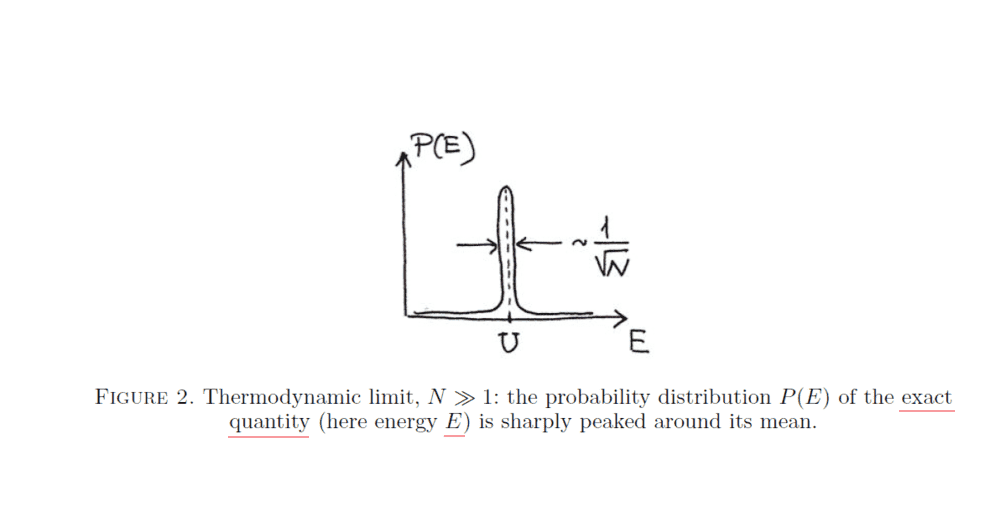
It represents the distribution (probability density function) of the kinetic energy $E$ (a random variable) of all the gas particles (i.e., $E=\sum_{i}^{N} E_{i}$, where $E_{i}$ (also a random variable) is the kinetic energy of gas molecule $i$, and $N$ is the total number of gas molecules). $U$ above is the mean value of $E$ ($U=\langle E\rangle$).

The author claims that the width of the distribution above is approximately $\frac{\sigma _{E}}{\langle E\rangle}=\frac{\langle (E-\textrm {U})^{2} \rangle ^{1/2}}{\langle E\rangle}$. Where does this approximation come from? Shouldn't it be just $\sigma _{E}=\langle (E-\textrm {U})^{2} \rangle ^{1/2}$?

The exact quote reads,

the distribution of the system's total energy $E$ (which is a random variable because particle velocities are random variables) is very sharply peaked around its mean $U=\langle E\rangle$: the width of this peak is $\sim \Delta E_{rms}/U \sim \frac{1}{\sqrt{N}}$ . This is called the thermodynamic limit— the statement that mean quantities for systems of very many particles approximate extremely well the exact properties of the system.

$\Delta E_{rms}$ above is just $\sigma _{E}$.

 

[vanhees71]

Are you aware of the central-limit theorem? It says that the sum of a large number of equally distributed random numbers to a very good approximation follows a Gaussian distribution with mean $U=\langle E \rangle =N \langle E_1 \rangle$ and standard deviation $\Delta E=\Delta E_1 \sqrt{N}$ (corrected in view of #3). The standard deviation is defined by $\Delta E^2 = \langle (E-U)^2 \rangle=\langle E^2 \rangle - U^2$.

 

[mjc123]

I think two things are being confused here.
If E is the total energy, i.e. E = ΣE_i, then <E> = N<E_i> and ΔE = ΔE_i*√N.
If E is the average energy per molecule, i.e. E = ΣE_i/N, then <E> = <E_i> and ΔE = ΔE_i/√N.

 

[vanhees71]

Sorry, of course you are right: $\Delta E=\sqrt{N} \Delta E_1$, but $\Delta E/E=\Delta E_1/(\sqrt{N} \langle E_1 \rangle)$, where $E$ is the total energy.

 

[Aaron121]

The question was not really about why $\frac{\Delta E_{RMS}}{\langle E\rangle}$ can be approximated by $\frac{1}{\sqrt{N}}$. But, rather, about why the author says the width of the distribution is, approximately, the ratio of the standard deviation to the mean $\frac{\Delta E_{RMS}}{\langle E\rangle}$, rather than just the standard deviation itself $\sigma_{E}=\Delta E_{RMS}$, which we all know measures how spread (how wide) a given distribution is.

 

[vanhees71]

I'd say the argument is to consider the (order of magnitude) of the width compared to the (order of magnitude) of the mean of the quantity. In other words you consider the mean an "accurate description" the smaller the standard deviation of the quantity is relative to the magnitude of the quantity itself.

 

[Aaron121]

@vanhees71

you consider the mean an "accurate description" the smaller the standard deviation of the quantity is relative to the magnitude of the quantity itself.

Correct me if I'm wrong, but do you mean by this that the standard deviation can be approximated by the mean when we have a very small standard deviation?

 

[Stephen Tashi]

In these lecture notes about statistical mechanics, page $10$, we can see the graph below.

View attachment 255318

The author claims that the width of the distribution above is approximately $\frac{\sigma _{E}}{\langle E\rangle}=\frac{\langle (E-\textrm {U})^{2} \rangle ^{1/2}}{\langle E\rangle}$.

We have to understand what is being graphed on the x-axis. Those notes show calculation for the the relative root-mean-square fluctuation of energy, so I think the x-axis is not total energy, but rather total energy rescaled by dividing it by the mean energy.

 

[Aaron121]

@Stephen Tashi

the x-axis is not total energy, but rather total energy rescaled by dividing it by the mean energy.

No where in the notes is it indicated that the graph is the plot of $P(E)$ against$E/U$. Had it been the case, the x-axis would not have been labeled $E$. Besides, it is clearly indicated under the graph that it is the plot of$P(E)$ against the energy $E=\sum_{i}^{N}(\frac{mv_{i}^2}{2})$.

 

[Stephen Tashi]

Besides, it is clearly indicated under the graph that it is the plot of$P(E)$ against the energy $E=\sum_{i}^{N}(\frac{mv_{i}^2}{2})$.

Then the notation that the width of the peak is proportional to $\frac{1}{\sqrt{N}}$ is incorrect.

The notes focus on "the thermodynamic limit". Trusting Wikipedia:

The thermodynamic limit, or macroscopic limit,[1] of a system in statistical mechanics is the limit for a large number N of particles (e.g., atoms or molecules) where the volume is taken to grow in proportion with the number of particles.[2] The thermodynamic limit is defined as the limit of a system with a large volume, with the particle density held fixed.[3]

As we increase the number of particles, the mean of the total energy $U$ will approach infinity and the standard deviation of total energy will also approach infinity.

If we want a graph where the the width of the peak about the mean decreases with the number of particles, we must look at quantities like the mean energy per particle or the distribution of some quantity that approaches a finite limit as $N$ approaches infinity. The notes derive the proportionality of $\sigma_E/ U$ to $\frac{1}{\sqrt {N}}$. The notes don't say that $\sigma_E$ is proportional to $\frac{1}{\sqrt{N}}$.

 

[vanhees71]

Of course, in the thermodynamic limit only quantities like the energy and particle density make sense. Of course in real-world systems the volume, the number of particles, the total energy etc. are all finite, the limit "$V \rightarrow \infty$" is a mathematical tool to formalize the simplifying description (and it's far from trivial, as already the treatment of an ideal gas in quantum many-body theory shows, which is only the most simple exactly treatable example).