lechris
- 4
- 0
Hello everyone,
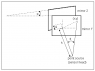
i am simulating a Michelson interferometer, where one mirror is slightly tilted, see picture.. This results in circular arcs / hyperbolic cross-section fringes. The center of these fringes depends on the focal length i am using, see picture.
Is there an analytical expression for the center of these fringes in dependency of the focal lenght?
Are there books that show the closed-form expression for such hyperbolic fringes / Fizeau fringes (so far i haven't found anything in the common literature).
Would be great if anyone has some insights on this.
Thanks!
i am simulating a Michelson interferometer, where one mirror is slightly tilted, see picture.. This results in circular arcs / hyperbolic cross-section fringes. The center of these fringes depends on the focal length i am using, see picture.
Is there an analytical expression for the center of these fringes in dependency of the focal lenght?
Are there books that show the closed-form expression for such hyperbolic fringes / Fizeau fringes (so far i haven't found anything in the common literature).
Would be great if anyone has some insights on this.
Thanks!