Optimal Painting Height for Maximum Viewing Comfort | 3m Viewing Distance

[acidxc]

hi,
can someone help me on 1 question i have been really trying and don't seem to know how to do it here is the question;

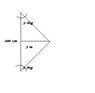
Francis is hanging a painting on a wall, he wants the height on the center of the painting to be located so that no visiors need to look up or down more the 5 degrees to viwer the center of the painting when standing 3 m away. If he expects visitors eyes to be between 152 cm to 200 cm off the ground. What is the range of heights that he can hang the center of the painting, to the nearest centimeter

So far i have done the following iam not sure if its the right start

x

 

[HallsofIvy]

Your picture is wrong. I presume that the vertical line labeled "200 cm" on the left represents the picture. You are told "no visiors need to look up or down more the 5 degrees to viwer the center of the painting when standing 3 m away" and that "he expects visitors eyes to be between 152 cm to 200 cm off the ground". You should have two lines drawn from the center of the picture to a vertical line 3 m away-one up to a height 200 cm, the other down to a height 152 cm. In other words, you should have a triangle with vertex at the center of the picture, vertical side of length 200- 152= 48 cm and base angles of 5 degrees. If you draw a horizontal line from the lower end of that vertical 48 cm line, representing the eyes of the shortest person, you have a right triangle with angle 5 degrees and near side 3 m= 300 cm. The opposite side is the height above that persons eyes (152 cm) to the center of the picture. Adding 152 to that will give the height of the center of the picture above the floor.