Optimization Problem with an RC BP filter

[The Electrician]

Do you understand what I mean by a cascade of two of your original circuits? I mean this:

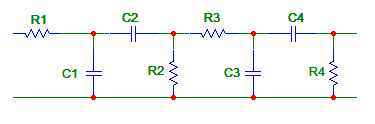
You will need to find the transfer function of this bandpass filter, and that will involve mucho algebra, if you know what I mean. This will be so difficult that I find it hard to believe that a "electronics for scientists" course would expect you to derive the transfer function for a 4th order passive network. Could there be another circuit that the professor expects you to use? Something easier to analyze?

How did you come up the original R1/C1/R2/C2 circuit? Did you professor give it to you?

 

[BiGyElLoWhAt]

It was one that I'd seen before. About a week or so before the assignment we talked about what the graph of the output would look like. There might be other circuits, but he explicitly told me only capacitors and resistors, as my original idea was an RLC circuit.

 

[The Electrician]

Can you see the pdf file in post #60?

 

[BiGyElLoWhAt]

Also, I think my initial setup was bad. I need to multiply by a term to get the current divided between the two branches. I basically have (Current through the whole circuit)* Impedance of the capacitor. That answer [edit** in the attached pdf] is the same as was posted earlier (by you or somebody else, I don't remember). I've never seen a transfer function left with a complex denominator before, though.

 

[BiGyElLoWhAt]

Yes.

 

[BiGyElLoWhAt]

Perhaps it is a bit extreme to do a O(4) circuit, but to put it in perspective, this is a 300 level course. A 500 lvl course that I took a couple years ago (as an elective (?)) had us analyze the salen key low pass filter, which was chalkboards and chalkboards and chalkboards of algebra.

 

[The Electrician]

The reason you need to do a 4th order circuit is because you have been constrained to use only Rs and Cs--no inductors, no opamps. With the low Q of a RC only network, the rolloff rate of a 2nd order is not fast enough to meet your requirements.

 

[The Electrician]

I've never seen a transfer function left with a complex denominator before, though.

It's typical among EEs, Rationalizing the denominator just adds complication. When evaluating an expression in complex arithmetic, nowadays a modern software such as Matlab, Mathematica, Maple, Mathcad, etc., is used and it's not useful to rationalize the denominator. The software can evaluate an expression with a complex denominator just fine.

 

[BiGyElLoWhAt]

So if I use 2 lowpass and 2 highpass, I'm not understanding conceptually how that will necessarily fix the problem. So I'm basically limited by the second derivative of the graph, right? V out vs. omega. By adding in another lowpass, in attempts to steepen the peak, one would be tempted to set "unity" at a higher frequency to have a steeper dropoff at the left. Won't this then mess with my peak at 10k?

 

[BiGyElLoWhAt]

Perhaps that's unique to physicists, then.

 

[The Electrician]

The center frequency stays the same, but the rolloff rate is enough higher to meet your requirements. Unity remains at 10 kHz.

 

[BiGyElLoWhAt]

Oh, because all the gains on the LHS of the vertex will be less than 1 and multiplied, and same with the RHS. Correct? So would both my lowpass filters have the same RC values?

 

[BiGyElLoWhAt]

Ignore that picture, it is as of now irrelevant. It was an attempt to explain my confusion.

 

[The Electrician]

Here's the response of the 2nd order network (blue; your original network), and the 4th order network (red):

 

[BiGyElLoWhAt]

Yes, yes. I think I get it now. What would be a reasonable, physical approximation that I could use to get my values? I.e. how I was trying to maximize it at 10k by setting both circuits in phase with each other and they would maximize due to superposition or something along those lines, or as was mentioned early where z_1 = R_1 at 3k, etc.

 

[The Electrician]

So would both my lowpass filters have the same RC values?

The product of each RC pair will be the same, placing the cutoff frequency of all the pairs at 10 kHz. But the impedance level of each pair should increase as you move to the output of the overall network. The increase of impedance level of a subsequent pair is achieved by increasing the value of R by some factor, such as 10, and decreasing the value of C by the same factor, but keeping the RC product constant.

 

[BiGyElLoWhAt]

Is that to minimize the impact on the current through the other branches, or on your supply?

 

[The Electrician]

Yes, yes. I think I get it now. What would be a reasonable, physical approximation that I could use to get my values? I.e. how I was trying to maximize it at 10k by setting both circuits in phase with each other and they would maximize due to superposition or something along those lines, or as was mentioned early where z_1 = R_1 at 3k, etc.

You could start out with the R1 and C1 values I gave in post #25. Subsequent RC pairs have increasing impedance level as I explained in the previous post.

The ideal is that the RC product gives a time constant so that the peak frequency of the network is 10 kHz. You don't worry about trying to make the attenuation of the network at 3 kHz and 30 kHz some value you would like. You have no control of those because the Q of a passive RC network is low and nothing can be done to increase it (normally using an opamp would be what you would do to increase Q).

The reason for increasing the impedance of successive RC pairs is to prevent the later pairs from loading the previous ones and degrading Q more than it already is with passive RC networks.

Cascading two of your original networks is the only way to get a faster rolloff rate. There is no way to "optimize" other than cascading.

 

[BiGyElLoWhAt]

What's a reasonable threshold to call something at "unity"? I think I get what I need to do, now. Thanks.

 

[The Electrician]

What's a reasonable threshold to call something at "unity"? I think I get what I need to do, now. Thanks.

What I've done in the two curves you see above is normalize the response of the network at 10 kHz, so the response at 10 kHz is always unity. This is a typical way of showing filter responses.

 

[BiGyElLoWhAt]

But that's only theoretical, right? You can't actually get the gain to be 1.

 

[The Electrician]

But that's only theoretical, right? You can't actually get the gain to be 1.

Of course. That's one of the things opamps can do for you.

 

[BiGyElLoWhAt]

Only if you rail it, though. And then it's railed to whatever your V is across the op amp. With this passive circuit, if I set .95Vin at 1k to the left and .95Vin 1k to the right (so 9k and 11k), would that seem reasonable?

 

[The Electrician]

If you have a look at the curves in post #74 those are what you get if the impedance levels of the various RC pairs are increased enough at each subsequent stage to avoid loading the previous stage. I'm not sure what you mean when you ask if .95 Vin at ± 1 kHz on either side of 10 kHz is reasonable. It's not a question of reasonableness. If you normalize the response of the filter to be unity at 10 kHz, the response on either side of 10 kHz is what it is.

The actual, un-normalized "gain" of your original circuit at 10 kHz is about .49.

Here's the un-normalized response of your original circuit using the R and C values I gave in post #25:

 

[BiGyElLoWhAt]

I didn't realize you were actually normalizing the graph. If I used the phrase normalize, that's my mistake, it wasn't my intent. I was thinking you were getting a lot closer to Vin than you were.

 

[The Electrician]

These passive RC filters have substantial loss even at the frequency of maximum "gain".

So I think you see what you must do now. I don't know any other way to get the "gain" at 3 kHz and 30 kHz to be less than 1/2 the "gain" at 10 kHz other than to cascade two of your original circuit.

I assume your professor is expecting you to demonstrate that your proposed circuit does in fact have the required relative attenuation at 3 kHz and 30 kHz.

 

[BiGyElLoWhAt]

I believe so, as well. Thanks for all your help. I actually think some things clicked in this last hour or so. Thanks a million.

 

[The Electrician]

When you derive a transfer function for a network don't waste time rationalizing the denominator, or any other simplifications. Just leave it in any form and use Matlab or a calculator that can do complex arithmetic to evaluate the transfer function. You should have a transfer function in terms of ω. Just set ω to 2*pi*f and evaluate the transfer function at 3 kHz, 10 kHz and 30 kHz to see if your requirements are met.

 

[BiGyElLoWhAt]

Thanks, will do.

 

[The Electrician]

If you find out that your professor had a solution that is much easier to analyze, would you please post it here?