CharlesDamle
- 17
- 3
- TL;DR Summary
- Find least total defects of companies using Bayes formula.
Hello!
I'm sitting with a problem that is causing me some troubles..
First part is using Bayes formula.
We have 3 companies that produce some apparatus. Each company has some defective percentage.
1) Suppose we pick up a defective apparatus. What is the probability it came from company A?
Here I use Bayes formula:
Defining the production in fractions.
Calculating the conditional probability (PD) and finding the probability it came from company A (PAD) to be 31%
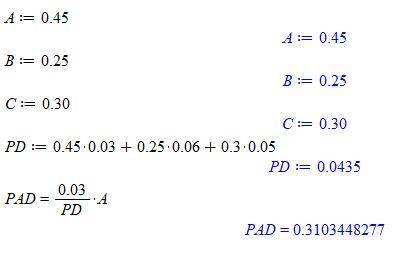
2) If a defective apparatus is found, which company is most likely to have produced it?
Here I just calculate it for all three and find it is most likely company B and C

3) Now assume all the facilities have the same probability of being identified with a defect apparatus.
We want the least total defective apparatus and keep the production percentages the same.
How does the percentage of defects change for each company? The defective rates can only increase.
This is the one causing me problems.
The way I tried to solve it, was to setup 3 Bayes equations with 3 unknowns, namely the new defective rates.
They are all equal to the same, as they are asked to have the same probability -> P = 1/3
I end up with this, where x1, x2 and x3 represents the respective companies (A, B and C).
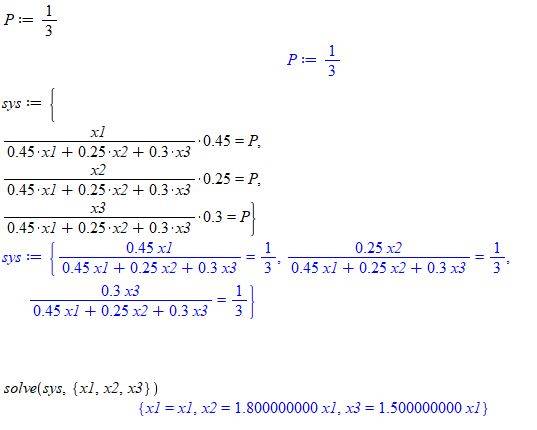
However this assumes that the defective rate of company A (x1) remains constant, and it says in the problem description it can only increase.
Am I even on the right track? I feel like I have to differentiate, but I'm now sure what.
I'd appreciate any advice or hints and sorry for the long post.
Cheers!
I'm sitting with a problem that is causing me some troubles..
First part is using Bayes formula.
We have 3 companies that produce some apparatus. Each company has some defective percentage.
| Company | Produced (%) | Defective (%) |
| A | 45 | 3 |
| B | 25 | 6 |
| C | 30 | 5 |
1) Suppose we pick up a defective apparatus. What is the probability it came from company A?
Here I use Bayes formula:
Defining the production in fractions.
Calculating the conditional probability (PD) and finding the probability it came from company A (PAD) to be 31%
2) If a defective apparatus is found, which company is most likely to have produced it?
Here I just calculate it for all three and find it is most likely company B and C
3) Now assume all the facilities have the same probability of being identified with a defect apparatus.
We want the least total defective apparatus and keep the production percentages the same.
How does the percentage of defects change for each company? The defective rates can only increase.
This is the one causing me problems.
The way I tried to solve it, was to setup 3 Bayes equations with 3 unknowns, namely the new defective rates.
They are all equal to the same, as they are asked to have the same probability -> P = 1/3
I end up with this, where x1, x2 and x3 represents the respective companies (A, B and C).
However this assumes that the defective rate of company A (x1) remains constant, and it says in the problem description it can only increase.
Am I even on the right track? I feel like I have to differentiate, but I'm now sure what.
I'd appreciate any advice or hints and sorry for the long post.
Cheers!