Package sliding down a round surface

[Femme_physics]

Homework Statement

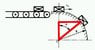
Packages, each one of them with a mass of 1kg, arrives from the moving track to a completely smooth surface of the runway, at a speed of 1 m/s, as described.

Calculate the max angle in which every package begins to veer off the runway track, if the radius of the track (R) is 0.5m

http://img691.imageshack.us/img691/2903/packagesz.jpg

The Attempt at a Solution

Sigma Fy = -W+N = 0
W = N = 9.81 [N]

N -> 0
Sum of all forces on x = ma

-Wsin(alpha) = m x v²/R

-9.81sin(alpha) = 9.81 x 1²/ 0.5

Sin^-1(2) = Math Error

?

 

[D_Tr]

You have to find the point at which the force required to hold the package on the track (this forve points towards the center of the circle) becomes greater than the component of the weight of the package pointing towards the center.

The "required" force is Fr = m*(v^2)/r (1)
The component of the weight towards the center is: Fgc = m*g*cos(φ)

(1) becomes: Fr = m*(v0^2 + vy^2)/r

if you find the vy as a function of height (potential -> kinetic energy) and then as function of cos(φ), you can equate the 2 forces and solve for cos(φ)

 

[I like Serena]

Hi Fp!

The normal force N is always perpendicular to the surface, so your sum of Fy is not right.

Btw, what is alpha?
I only see an angle marked phi_max.

I think an FBD might be helpful...

And you used v = 1 m/s, but when the package has slid down the runway, its speed will have increased.
By how much?

 

[Femme_physics]

The normal force N is always perpendicular to the surface, so your sum of Fy is not right.

Ah, well to be fair I did correct myself in the other equation where I give W an angle.

Btw, what is alpha?
I only see an angle marked phimax.

Yes, I just took it upon myself to rename it because I never remember the name of that greek sign. Phi. Phi. Phi.

I think an FBD might be helpful...

I think you're right.


http://img638.imageshack.us/img638/8999/fdbd.jpg

And you used v = 1 m/s, but when the package has slid down the runway, its speed will have increased.
By how much?

I got 2 unknowns, delta y and Vb!

http://img40.imageshack.us/img40/3954/fdb2.jpg

 

[I like Serena]

Good mooooooorning, Fp!

Yes, I just took it upon myself to rename it because I never remember the name of that greek sign. Phi. Phi. Phi.

Lemme hear that just a couple more times? :P

I got 2 unknowns, delta y and Vb!

Well, there's really relevant one unknown, that is phi, which you want to find.

What is delta y in terms of phi?

And then, what will v be at the angle phi?

Ah, well to be fair I did correct myself in the other equation where I give W an angle.

Good. :)

So what is the resultant radial force in terms of phi?

 

[Femme_physics]

Good morning cowboy!

Well, there's really relevant one unknown, that is phi, which you want to find.

What is delta y in terms of phi?

And then, what will v be at the angle phi?

Hmm.. I need to use the last equation to the left for that, right?

Good. :)

So what is the resultant radial force in terms of phi?

But N goes to zero, so the only force playing a role is gravity. So, come to think of it, you should really ignore N in my FBD!

 

[I like Serena]

Hmm.. I need to use the last equation to the left for that, right?

Nooooo, you already had the right formula in your last scan.
In your table that is the formula on the bottom right. ;)

But N goes to zero, so the only force playing a role is gravity. So, come to think of it, you should really ignore N in my FBD!

Yes, I guess you can. :)

But what is the radial component of the force of gravity then?

Does it give an acceleration that is enough to keep it in circular motion?

 

[Femme_physics]

Does it give an acceleration that is enough to keep it in circular motion?

Well, how am I suppose to know that if I'm not given the value of max acceleration where the object will stay in circular motion?

 

[I like Serena]

Well, how am I suppose to know that if I'm not given the value of max acceleration where the object will stay in circular motion?

Didn't you have yet another formula for that?
The formula for centripetal acceleration?

 

[Femme_physics]

Didn't you have yet another formula for that?
The formula for centripetal acceleration?

Fcentripetal = m x v^2/R

I don't have V, so I can't find F centripetal

As far as

http://img40.imageshack.us/img40/3954/fdb2.jpg

I still don't see how to use it without delta y

What is delta y in terms of phi?

Well, I can only come up with this equation for phi(max)

http://img268.imageshack.us/img268/1681/anglemax.jpg

Still feel like am stuck with 3 equations that have nothing to do with each other! How to make them come together is a bit beyond me...help?

 

[I like Serena]

Still feel like am stuck with 3 equations that have nothing to do with each other! How to make them come together is a bit beyond me...help?

Ok. We'll take it step by step.
First is delta y.

The problem asks for \phi_{max}.
We don't know it yet, so we'll take along as an unknown variable (1 unknown!).

Delta y is the vertical distance from the top of the runway to the position the package will have when it is at the angle \phi_{max}.

Use trigonometry to find this distance?

 

[Femme_physics]

I understand that d2 is the height I'm looking for.http://img62.imageshack.us/img62/5315/igei.jpg

but I have no information with respect to the angles and the distances. How can I use trigonometry without ANY lengths and angles?

 

[I like Serena]

I understand that d2 is the height I'm looking for.

Yes. :)

but I have no information with respect to the angles and the distances. How can I use trigonometry without ANY lengths and angles?

So let's introduce an angle and give it a name.
Let it start at the top of the ramp, and let it end at some current position of the package.
Let's call it... phi.

Do you like the name phi? :shy:

Now to calculate d2 we also need the radius of the trajectory.
Do you have that one already?
Let's call it R, or just 0.5 m, if you prefer that.

 

[Femme_physics]

Do you like the name phi?

*grins*

Yes, yes I do.

But I don't see how the radius of the trajectory helps us calculate d2. Look at the triangle I draw, nothing there equals the radius

 

[I like Serena]

*grins*

Yes, yes I do.

But I don't see how the radius of the trajectory helps us calculate d2. Look at the triangle I draw, nothing there equals the radius

Let's pick another triangle then.

Say one that has phi as in the following picture, and that has R as in the same picture.

We'll use a triangle that has the drawn line to the package as the diagonal side.
Another side goes straight up until it reaches the level of the package.
And the third and final side a the horizontal line on the level of the package.

 

[Femme_physics]

Wow, thanks for the awesome effort!

I see it now, and after finding the opposite I can do Radius minus the opposite to find the value I need! Brilliant :D

But I still have only one length for this right triangle, I can't get very far from this.

 

[I like Serena]

Wow, thanks for the awesome effort!

Yeah, well, at first I wanted to put only a hyperlink in, pretending it was a giant effort, that would simply show your original picture.
But then I though I might as well extend that giant effort with a minor adjustment to the picture (and I like red).

I see it now, and after finding the opposite I can do Radius minus the opposite to find the value I need! Brilliant :D

Right!
(That is, with the adjacent! )

But I still have only one length for this right triangle, I can't get very far from this.

Ah, but the length R and the angle phi fully determine this right-angled triangle.

Can you write down the definition of \cos(\phi), using R for the hypotenuse?

 

[Femme_physics]

cos phi = adjacent/radius

Hmm...so that equation and sigma Fy is the way to find the answer?

 

[I like Serena]

Hmm...so that equation and sigma Fy is the way to find the answer?

Huh? I don't think we need sigma Fy.
What do you want to use sigma Fy for?

cos phi = adjacent/radius

Yes, so:
adjacent = R \cos(\phi) = 0.5 \cos(\phi)

And, as you said, delta y is R minus the adjacent. So:
\Delta y = 0.5 - 0.5 \cos(\phi)

So we have delta y!
And just 1 unknown (phi) that we're taking along with us.


Now for the speed of the package.
Do you know how to calculate that?
Because that is what we needed delta y for...

 

[Femme_physics]

Oh my, I didn't know you replied! I thought you left me hanging here from some reason lol. Sorry, I'll get to it now as well^^
I don't like leaving things unsolved. Esp. one day before the test!

 

[I like Serena]

Oh my, I didn't know you replied! I thought you left me hanging here from some reason lol. Sorry, I'll get to it now as well^^
I don't like leaving things unsolved. Esp. one day before the test!

Hey there!

Actually, I think there are currently 4 recent threads where you left me hanging (including this one).
I was wondering if you'd ever get to them or if you had decided to move on (which is fine if that's what you want - you decide! ).

Edit: Btw, when I'm at work I'm limited in my ability to respond, and if you don't respond yourself, I'm less inclined to make time.

 

[Femme_physics]

Can you PM me which threads did I miss?

 

[Femme_physics]

I don't know how to find V since I only have 1 equation, and 2 unknown (the angle and Vfinal)

http://img29.imageshack.us/img29/9629/cosemek.jpg

 

[I like Serena]

The initial speed is given as 1 m/s.
So from that you can find the final speed, with just phi as unknown, which you're still taking along.

From the final speed you can calculate the centripetal acceleration (still taking phi along).

The next step is to find the part of the weight W that is pointed inward, in the direction of the center of the circle.
This will also have phi in it, which again, we're taking along.

The last step is the equation where you set the part of the weight W that is pointed inward equal to the centripetal force times the mass.
This one you can finally solve to find phi.

 

[Femme_physics]

LOL doesn't sound that simple. I'll be forced to leave this one hanging, I'm not sure if I'd want to solve more mechanics problems after the test (which is in 2 more hours!), at least not rigid material ones. We'll see.^^

Thanks for all your amazing help!

 

[I like Serena]

Ah well.
I'll type in the solution then, so you can use it as a reference.

 

[Femme_physics]

Too late. SMS it lol just leaving

 

[I like Serena]

With trigonometry:
\Delta y = R - R \cos \phi = 0.5 - 0.5 \cos \phi

Calculate the final velocity, keeping phi:
\frac {v_f^2} 2 = \frac {v_i^2} 2 + g \Delta y

Fill the numbers in and substitute delta y:
\frac {v_f^2} 2 = \frac {1^2} 2 + 9.81 (0.5 - 0.5 \cos \phi)
\frac {v_f^2} 2 = 5.405 - 4.905 \cos \phi

Multiply left and right with 2:
v_f^2 = 10.81 - 9.81 \cos \phi

Centripetal acceleration:
a_{centripetal} = \frac {v^2} R

Plugging in our v_f²:
a_{centripetal} = \frac {10.81 - 9.81 \cos \phi} {0.5} = 21.62 - 19.62 \cos \phi


Calculate the radial force from W, keeping phi:
F_{radial} = W \cos \phi

Filling in W = 9.81 N:
F_{radial} = 9.81 \cos \phi

The radial force must equal the centripetal acceleration times mass
F_{radial} = m a_{centripetal}

Filling in our previous results:
9.81 \cos \phi = 1 \cdot (21.62 - 19.62 \cos \phi)

Solve for phi:
\cos \phi (9.81 + 19.62) = 21.62
\cos \phi = 0.7346

So phi_max is:
\phi_{max} = 42.7^o


Am I still in time?
(Hope I didn't make a calculation error. )

Edit: Fixed the calculation errors.

 

[ehild]

I guess, there is a mistake in your solution somewhere.
It is better to use symbolical solution and plug in data at the end.

From conservation of energy:
\frac {v_f^2} 2 = \frac {v_i^2} 2 + g R(1-\cos\phi)

From centripetal force:
v_f^2=Rg\cos\phi
******
Rg\cos\phi=v_i^2 + 2 g R(1-\cos\phi)

\cos\phi=\frac{2}{3}+\frac{v_i^2}{3Rg}

ehild

 

[I like Serena]

I guess, there is a mistake in your solution somewhere.
It is better to use symbolical solution and plug in data at the end.

Agreed!

I just didn't want to bring extra unknowns along that might confuse the OP.
(And I was testing if the OP was sharp enough to see where the mistake is *cough*! )

Your solution looks much nicer and simpler!

 

[ehild]

Thanks. Check if 1/2+0.5*9.81=5.905

ehild

 

[I like Serena]

Done!
(And edited my full solution to eliminate the calculation errors.)

 

[Femme_physics]

You guys are incredible!

Test's over and I did very well. We're not going to study mechanics next semester. So, I just want to say big thanks^^ Next year I might be the tutor for the 1st year mechanics students, so my adventures in the realms of basic mechanics might (or very probably) not be over yet. I still have a few holes to fill, but I think I'll worry about closing them later^^

This problem is definitely too big and too complex! Reminds me of the crashing airplanes, even though I eventually solved it. There have been a few questions throughout the year in our basic mechanics course considered controversially too difficult. This might as well be one of them!

 

[I like Serena]

Whaaaaaaat! But, but, but, ... you can't!
You can't stop doing mechanical problems! Sniff!
And btw, the planes didn't crash (WHOAA!), so there's still more stuff to see, to learn...

 

[Femme_physics]

They did crash, because the distance is so small! And, frankly, I'm already having a mechanical itch, so I'll never really stop doing mechanics, it's just that I'll be doing it from now on at a much slower pace!

So now I can be relaxed and go over this problem for instance and there was a 3D statics problem at the test that I'm still looking at how to solve it. So, this is for the best, since I can now invest more time and effort in a single problem, rather than shooting all over the place to get as much as I can. I think you'll like me better that way

 

[I like Serena]

I have no complaints about how much time and effort you invest in all of your problems!
And I like you any which way I can, as long as we're interacting. :shy:
Of course it helps if you make a drawing every now and then!
(And if you don't secretly remove a cord from a problem! )