Parallel Sheets and Electric Fields

[prototech]

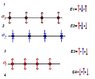
Homework Statement

[PLAIN]http://img532.imageshack.us/img532/1460/problemjh.png

Homework Equations

Electric field from infinite plane:
$$E = \frac{\sigma }{2\varepsilon _{0}}$$

The Attempt at a Solution

I'm pretty sure that at region 2, the total electric field is 0 since all the charges on the surface will distribute themselves. I've attempted drawing the vectors for the electric fields except for region 1. My work is the one in red.
[PLAIN]http://img62.imageshack.us/img62/149/problemattemp.png

 

[ehild]

Well, I can not follow your notations.
You know the surface charge density of the insulating plane, and Gauss Law predicts the electric field due to this homogeneous charge distribution. You draw correctly that the electric field lines are normal to the planes. As the field lines can start and end only in charges, and the field is homogeneous and normal to the the plane at the insulating sheet, it must be the same in the whole region 3.
You are also right stating that E=0 inside the metal plate. You can apply Gauss' Law: What should be the charge density on the bottom surface of the metal sheet? The metal is neutral, so what is the surface charge density on the top surface? What is the electric field strength then in region 1?

ehild

 

[prototech]

I believe at the top of the conducting sheet is the charge density is +σ and at the bottom the sheet is -σ.

Sorry about the notation. I was trying to use region 2 to calculate the magnitude of the electric field vectors and use superposition. At region 2, the total electric field is 0. E1 is the electric field caused by the + charges on the insulating plate (σ1). E2 and E3 come from when I assume that the top conductor is neutral: |σ2| = |σ3| (magnitude of the charge densities are equal, but they have opposite directions: σ2 = -σ3).

Using the fact that at region 2 the total electric field is 0, so:
$$\vec{E}_{tot} = \vec{E}_{1} - \vec{E}_{2} - \vec{E}_{3}$$

$$\frac{\sigma_{1} }{2\varepsilon _{0}} - \frac{\left |\sigma_{2} \right | }{2\varepsilon _{0}} - \frac{\left |\sigma_{3} \right | }{2\varepsilon _{0}} = 0$$

$$\frac{\sigma_{1} }{2\varepsilon _{0}} - 2\frac{\left |\sigma_{2} \right |}{2\varepsilon _{0}} = 0$$

$$\left |\sigma_{2} \right | = \frac{\sigma }{2}$$

So I found the magnitudes of the electric fields. Now I guess I just needed to then find the directions of the electric fields and then take their sum at their regions. So far, I think regions 1 and 4 have the same electric fields and they're both negative from they way I drew the vectors. Region 3 is positive because the vectors E2 and E3 cancel, leaving E1.

 

[ehild]

I see now what you did. You replaced the metal sheet with two homogeneously charged parallel planes. Do not forget that the electric field lines originate from positive charges or come from infinity, and they end in the negative ones or in infinity. It is true that sigma(2) and sigma(3) are half of sigma(1), but sigma(2) has to be negative and sigma(3) positive.

I redraw your picture, to make it a bit more clear for me. The arrows at the charges show the field lines emerging from or entering to them. The field is opposite at the opposite sides of a charged plane.

Now it is easy to decide the resultant field vector in all region.

ehild