cherry
- 25
- 6
- Homework Statement
- A curve given parametrically by (x, y, z) = (3 - t, -1 - 3t^2, 2t + 2t^3). There is a unique point P on the curve with the property that the tangent line at P passes through the point (2, 8, 12). What are the coordinates of point P?
- Relevant Equations
- (x, y, z) = (3 - t, -1 - 3t^2, 2t + 2t^3)
My work so far:
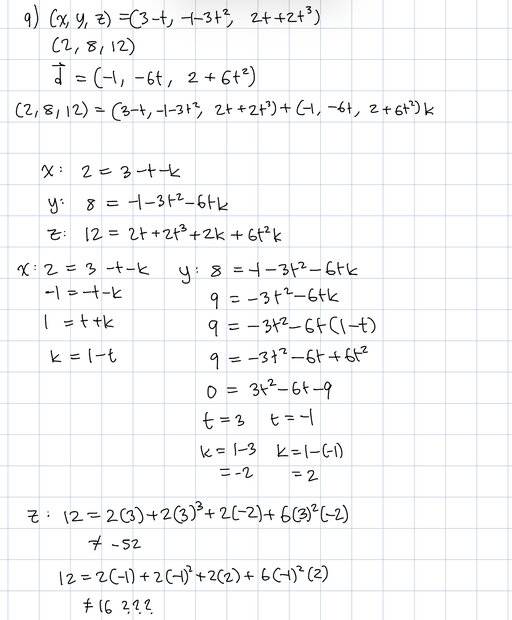
I am stuck because when I inputted the two possible values of t and k, neither solution worked. Where did I go wrong? Pointers would be appreciated! :)
I am stuck because when I inputted the two possible values of t and k, neither solution worked. Where did I go wrong? Pointers would be appreciated! :)
 ##\qquad## !
##\qquad## !