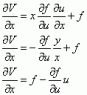iAlexN
- 16
- 0
Given V=xf(u) and u = \frac{y}{x} How do you show that:
x^2 \frac{\partial^2V}{\partial x^2} + 2xy\frac{\partial^2V}{\partial x\partial y} + y^2 \frac{\partial^2V}{\partial y^2}= 0
My main problem is that I am not sure how to express V in terms of a total differential, because it is a function of x and f(u). So it depends on a variable and a function, and doesn't x also depend on u and y?
dV = \frac{\partial V}{\partial x} * dx + \frac{\partial V}{\partial f(u)} * f(u)
This total differential doesn't really help much, there must be some other way of writing it down and simplifying it?
So how should you go about solving this?
x^2 \frac{\partial^2V}{\partial x^2} + 2xy\frac{\partial^2V}{\partial x\partial y} + y^2 \frac{\partial^2V}{\partial y^2}= 0
My main problem is that I am not sure how to express V in terms of a total differential, because it is a function of x and f(u). So it depends on a variable and a function, and doesn't x also depend on u and y?
dV = \frac{\partial V}{\partial x} * dx + \frac{\partial V}{\partial f(u)} * f(u)
This total differential doesn't really help much, there must be some other way of writing it down and simplifying it?
So how should you go about solving this?