Perihelion Shift in Near-Circular Orbits: 6πm/a + Higher Order Terms

[Jorrie]

The full power series for the Schwarzschild portion of perihelion shift is given in Mathpages as:

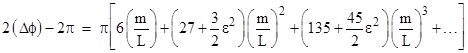
where L = a(1-\epsilon^2), a the semi-minor axis and \epsilon the eccentricity. This implies that as \epsilon tends to zero, the perihelion shift tends to a non-vanishing 6\pi m/a + some much smaller higher order terms.

If we do an angular acceleration derivation for a Schwarzschild orbit (d^2\phi/dt^2), I have arrived at
\frac{d^2\phi}{dt^2} = \frac{-2v_r v_\phi}{r} \frac{r-3m}{r-2m}
where v_r=dr/dt and v_\phi=d\phi/dt (geometric units: c=G=1)
Pervect and CarlB have arrived at equivalent results in this old orbital acceleration thread.

My question is that since d^2\phi/dt^2 goes to zero when v_r goes to zero for the circular orbit, how is this compatible with the non-vanishing perihelion shift above?

 

[Orodruin]

Why do you think there is a contradiction here? The circular orbit does not have a perihelion - all points on the orbit are at the same distance from the central object and therefore the angular velocity must be constant.

 

[Jorrie]

Why do you think there is a contradiction here? The circular orbit does not have a perihelion - all points on the orbit are at the same distance from the central object and therefore the angular velocity must be constant.

The question is then: is the power series from Mathpages giving the perihelion shift inadequate?

 

[Orodruin]

The question is then: is the power series from Mathpages giving the perihelion shift inadequate?

No. Again I do not understand why you would think there is a contradiction here. The limiting orbit has perfectly circular shape and such an orbit has constant angular velocity. There is no black magic here. If you perturb it ever so slightly you get an orbit with a perhelion shift.

 

[Jorrie]

The limiting orbit has perfectly circular shape and such an orbit has constant angular velocity

I agree, but this is not what the power series says is the limiting case. It gives an 'invisible' shift of 6 pi m/r. Which again raises my question: is the series inadequate, e.g. to describe orbits with extremely small eccentricities?

 

[Orodruin]

I agree, but this is not what the power series says is the limiting case. It gives an 'invisible' shift of 6 pi m/r. Which again raises my question: is the series inadequate, e.g. to describe orbits with extremely small eccentricities?

Why would you think the series would be inadequate? There is no contradiction anywhere in your expressions. You are misinterpreting and misrepresenting the results. The answer really was in my previous post.

Also, this is nothing different from what would occur in classical mechanics with a central potential different from the 1/r. It is just that the period of small oscillations around the circular orbit does not match with the orbital period.

 

[Jorrie]

Also, this is nothing different from what would occur in classical mechanics with a central potential different from the 1/r. It is just that the period of small oscillations around the circular orbit does not match with the orbital period

OK, I think I understand what you are saying. The amplitude of radial oscillations goes to zero, but not the period. So the lowest order peri-shift approximation in the series is independent of eccentricity (for constant L), but higher orders will show an eccentricity influence.

 

[Orodruin]

Talking about eccentricity influence is a bit misleading as the point is that the orbit is not an ellipse.

It might be more instructive to view things in terms of the relative periods between radial oscillations and the orbital period. The radial oscillations will have different periods depending on the amplitude as long as the effective potential is not harmonic.

 

[Jorrie]

Good point, thanks.