Gnomie
- 2
- 0
Hi all,
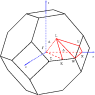
I'm currently trying to learn more about photonic band gaps. The material I am looking at is an FCC crystal of spheres with an (111) surface, and this structure is theoretically predicted to display an incomplete band gap from the gamma to L points. (Please see attachment)
Essentially I am trying to figure out how an incomplete band gap actually behaves compared to a complete band gap. A complete band gap of course reflects light of all angles of incidence while an incomplete does not. But which parts of the light actually gets reflected? For example, is it such that all light within a "cone" gets reflected (much like diffracted orders)? How can I translate the band structure information into actual real-space angles?
Thank you for your time,
Gnomie
I'm currently trying to learn more about photonic band gaps. The material I am looking at is an FCC crystal of spheres with an (111) surface, and this structure is theoretically predicted to display an incomplete band gap from the gamma to L points. (Please see attachment)
Essentially I am trying to figure out how an incomplete band gap actually behaves compared to a complete band gap. A complete band gap of course reflects light of all angles of incidence while an incomplete does not. But which parts of the light actually gets reflected? For example, is it such that all light within a "cone" gets reflected (much like diffracted orders)? How can I translate the band structure information into actual real-space angles?
Thank you for your time,
Gnomie