Browntown
- 18
- 0
- Homework Statement
- Physics Lab Propagation of Error Issue
- Relevant Equations
- ∂f/∂b=∂/∂b (tan^(-1)(a/4b))= 1/(1+(a/4b)^2 )×(-a)/(4b^2 )=1/(1+((5.922 cm)/(4×1.766 cm))^2 )×(-5.922 cm)/(4×(1.766 cm)^2 )
Homework Statement: Physics Lab Propagation of Error Issue
Homework Equations: ∂f/∂b=∂/∂b (tan^(-1)(a/4b))= 1/(1+(a/4b)^2 )×(-a)/(4b^2 )=1/(1+((5.922 cm)/(4×1.766 cm))^2 )×(-5.922 cm)/(4×(1.766 cm)^2 )
Hello,
I'm trying to find the uncertainty in a function from the lab manual for the critical angle of refraction and since this is my first time doing such a thing I'm a bit confused.
When I take the derivative of the inverse tan function provided and input my values, the units of cm don't seem to cancel and I can't figure out how to fix that
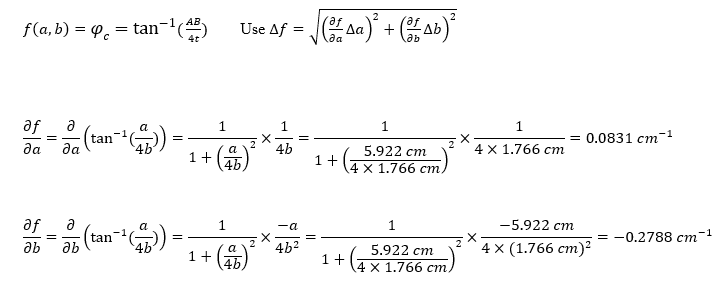
Homework Equations: ∂f/∂b=∂/∂b (tan^(-1)(a/4b))= 1/(1+(a/4b)^2 )×(-a)/(4b^2 )=1/(1+((5.922 cm)/(4×1.766 cm))^2 )×(-5.922 cm)/(4×(1.766 cm)^2 )
Hello,
I'm trying to find the uncertainty in a function from the lab manual for the critical angle of refraction and since this is my first time doing such a thing I'm a bit confused.
When I take the derivative of the inverse tan function provided and input my values, the units of cm don't seem to cancel and I can't figure out how to fix that