Pinhole Diffraction of a Spherical Wave

[Juliana Abrantes]

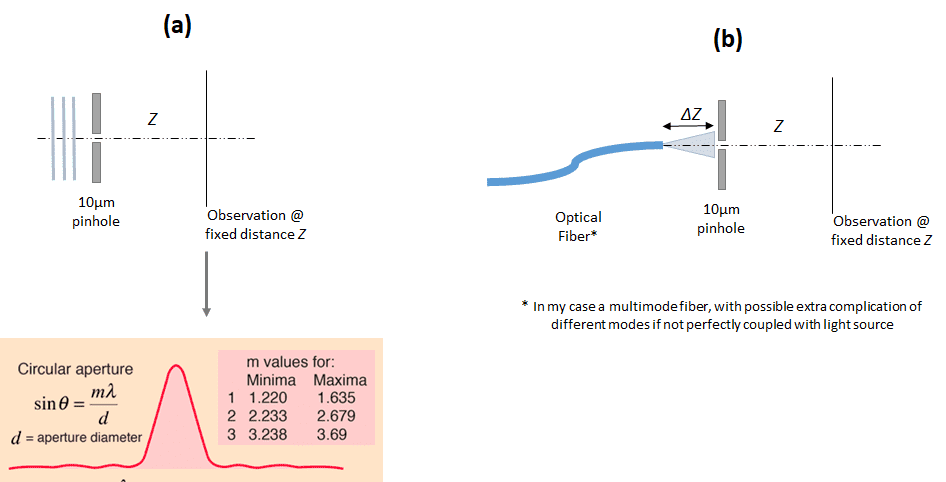
Case (a) is the textbook of a planar incident wavefront and below it in the figure is the known simple formula for the central spot and fringes, or minima and maxima, angular distribution with respect to the optical axis.

So, the question here is regarding case (b). The position (usually estimated angularly, Θ) of the central spot and consecutive fringes is always the same, depending only on pinhole diameter and wavelength, according to the eqn. sin(Θ) = m*λ/d?? Regardless of the shape of the incoming wavefront?

And also, if there is a different output pattern, is it dependent on ΔZ, the distance from the source (e.g. fiber tip) to pinhole? If you put them closer (smaller ΔZ) the throughput will definitely be higher, but are the central spot size and fringe positions going to change?

Thank you very much in advance!

 

[.Scott]

The key to "pin hole" is that the hole is not many wavelengths across - and it acts like a spatial filter, losing the directionality of the incident light from the source.

To the extent that it is large enough to allow some of the beam to pass with its directionality intact, that part of the beam will not be bending towards its counterpart from another pin hole.

A spherical wave striking two pinholes may not strike both at the same time, but neither would a planar wave.Clearly, if you place the spherical fiber optic output closer to the pinhole, more light will reach the pinhole.
At 10uM, you are working with a pin hole that is 15 or 20 wavelengths - enough for some spatial information to pass through. An experiment you can try is to placing the fiber optic output so that it strikes the pinhole at an angle - say 20 degrees from perpendicular (or hole the fiber steady and rotate the pin hole plate). Then look at the output. At 10uM, you should be able to see some affect on the output from this angle.

 

[Juliana Abrantes]

Thanks Scott.

Yes, but the spatial filter analogy would hold for the case in which I put a lens to focus the beam at the pinhole position, right?

In my case I am really interested in the effect on diffraction of the deltaZ change for the diverging wave scenario. Not the overall energy throughput, but on the geometrical fringe pattern, if there is any change at all.

By the way, the fiber NA is 0.22.

 

[Juliana Abrantes]

In other words, I wanted to know if there is a limit for this "loss of directionality" information Scott correctly mentioned when you have angles hitting the pinhole, with the fiber tip very close to it. And how it affects (if it does) the observed diffraction pattern.

 

[Lord Jestocost]

Maybe, I am not right, but I think that's the realm of Fresnel diffraction.
http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/fresnelcon.html#c1

 

[.Scott]

In other words, I wanted to know if there is a limit for this "loss of directionality" information Scott correctly mentioned when you have angles hitting the pinhole, with the fiber tip very close to it. And how it affects (if it does) the observed diffraction pattern.

Here is a paper that will provide some background:
http://www.phys.unm.edu/msbahae/Optics Lab/Fourier Optics.pdf

In approximate terms, you can think of your pin hole as a spatial filter aperture that is eliminating the spatial information beyond its $20\lambda$ diameter.

With a completely open aperture, light that is traveling straight through, perpendicular to the aperture will project onto a screen as a small well-defined spot. When the pin hole is applied, it is no longer possible for the spot to remain so well confined, because the higher spatial frequency information that defines its nice edges has been removed.

When the light is not traveling perpendicular to the aperture, it is also filtered - but because it is off center, it will be more dependent on those higher spatial frequencies. So we should expect it to be bigger than our first spot and spread out more in the direction directly to and away from the center point on the screen.

 

[Andy Resnick]

Summary: Literature and internet only talk about the very basic case of an incident planar wave... can someone help me with an equally basic but perhaps more tricky case of a spherical wave and the dependence of the diffraction pattern with the distance from source to pinhole?

The essential result you are interested in is that the far-field diffraction pattern, considering scalar diffraction only, is the Fourier Transform of the incident field. The case of a monochromatic plane wave is particularly simple- the Fourier transform of a square aperture is a sinc function (sin(x)/x), the Fourier transform of a circular aperture is a jinc function J(x)/x; often referred to as an'Airy function'.

For a monochromatic spherical wave incident on the pinhole, you have an incident field e^(ikz)/R, where R is the radius of the spherical wave. Clearly, unless R is about the same as the pinhole radius, the far-field diffraction pattern is nearly the same as for a plane wave. However...

We only discussed far-field diffraction and implicitly only a single 'image plane'. We also only discussed idealized sources (plane waves or spherical waves). The general case of scalar diffraction of an arbitrary field by an arbitrary aperture is the https://www.physics.byu.edu/faculty/berrondo/wt642/diffraction.pdf. If you have a partially coherent incident beam, the propagation of the beam can be quantified using the mutual coherence function. Going further to vector diffraction, I am not aware of a full solution. There is the Debye approximation, but that's about it.