MatinSAR
- 673
- 205
- Homework Statement
- Calculate the following terms.
- Relevant Equations
- Complex numbers.
$$Re(e^{2iz}) = Re(\cos(2z)+i\sin(2z))=\cos(2z)$$$$e^{i^3} = e^{-i}$$ $$\ln (\sqrt 3 + i)^3=\ln(2)+i(\dfrac {\pi}{6}+2k\pi)$$
Can't I simplify these more? Are they correct?
Final one:## (1+3i)^{\frac 1 2}##
Can I write in in term of ##\sin x## and ##\cos x## then use ##(\cos x+i\sin x)^n=\cos (nx)+i\sin (nx)##?
Something like this :
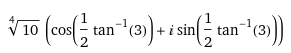
Many thanks.
Can't I simplify these more? Are they correct?
Final one:## (1+3i)^{\frac 1 2}##
Can I write in in term of ##\sin x## and ##\cos x## then use ##(\cos x+i\sin x)^n=\cos (nx)+i\sin (nx)##?
Something like this :
Many thanks.