Please, HELP ME indentify this equation

  • Thread starter Thread starter lgbarajas
  • Start date Start date
AI Thread Summary
The equation in question relates to acceleration in curved spaces or manifolds, as indicated by its appearance in the context of fictitious forces in curvilinear coordinates on Wikipedia. The discussion highlights a connection to virtual work, suggesting that the equation may involve summing virtual work across different directions. A user noted the importance of including a boldface "a" in front of the equation for clarity. The original poster found the equation on Wikipedia, prompting the inquiry for identification. The conversation emphasizes the need for context to fully understand the equation's application.
lgbarajas
Messages
1
Reaction score
0
Cannot recognize the use or description of this equation... can anyone help me?

Thanks in advance
 

Attachments

  • Ecuacion.png
    Ecuacion.png
    3.1 KB · Views: 587
Mathematics news on Phys.org
The gamma here is from tensor calculus. Everything outside the bracketed part reminds me of virtual work almost. It could be acceleration equals the sum of the virtual work in each k^th direction (plus some mixing up of the indices). Now, I haven't had enough tensor calculus to help you more; sorry.

I have a question though. Where did you find this equation? I have no context to work with here.
 
I thought about what I posted and then started searching for those key terms I talked about. I found the image on Wikipedia (the source of all knowledge) under the section on Fictitious Forces in Curvilinear Coordinates. It was the last equation given. I thought it was similar in form, so I posted it.

dbe726d8d53aa4fc458150c380535db4.png


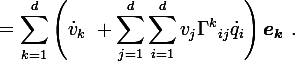
There should be a bold face a in front of the equation. Wikipedia says this is for acceleration in curved spaces/manifolds.

The website is:

http://en.wikipedia.org/wiki/Mechanics_of_planar_particle_motion

Hope that helped!
 
Last edited:

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Similar threads

A Does anyone recognize this equation?
Replies
3
Views
1K
B Why are the values (-1.618, 0) and (0.618 ,0) solutions for this equation?
Replies
44
Views
5K
Help with Recurrence Equation
Replies
4
Views
2K
MHB Solving Algebra equation 3x=15
Replies
4
Views
4K
I need sources to learn about dynamic systems
Replies
4
Views
2K
MHB Equation for tangent of the curve
Replies
1
Views
1K
MHB Height/diameter relationship of 19 (H8/D8=19)
Replies
2
Views
1K
I Why is (a+b)/2 not recommended in the Bisection method?
Replies
6
Views
1K
MHB Why Does Triangle AOB Have Angles of 30, 30, and 120 Degrees?
Replies
1
Views
1K
A Proving the Equivalence of Local and Global Maxima for Concave Functions
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top