Please help with PHYS-1 Problem Forces/Static/Equilibrium

[StudyBuddy]

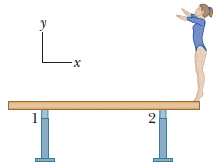
A gymnast with mass 56.5 kg stands on the end of a uniform balance beam as shown in the figure below. The beam is 5.00 m long and has a mass of 250 kg (excluding the mass of the two supports). Each support is 0.530 m from its end of the beam. In unit-vector notation, what are the forces on the beam due to support 1 and support 2?

Homework Equations

F=ma
Torque=I*alpha

and where there is no acceleration, the sums are equal to 0.

Setting up the forces as the following:
F1 = support 1
F2 = support 2
F3 = gravitational force in center of beam
F4 = force of the gymnast at the end

I used Newton 2 for the sum of the forces in equilibrium (acceleration = 0)...
F1+F2+F3+F4=ma=0 where F3 = (250kg*g), F4=(56.5kg*g)
F1+F2+306.5g=0
1.) F2=-F1-306.5g
Then Newton II for sum of the torques... Where L is the length of the beam, and point I will rotate is located at the point where the gymnast is, so I can simplify the calculations.

2.)F1*4.47m +F3*2.5m+F2*0.053m=0

Next, I plugged 1( solved F2) into (2)

Simplifying, I get F1=1150.52N
Please help, and thank you in advance for you time and generosity.

 

[TomHart]

For one, your work indicates that the support posts are positioned L/6 from the ends, but that isn't what is given in the problem. But it looks like your set up of the problem is good. I just think you made some errors in working through your equations. Based on the geometry of the problem, F1 is going to be less than F2. So yeah, your 2588 N for F1 is going to be too high.

 

[Student100]

What're you doing here?

I used Newton 2 for the sum of the forces in equilibrium (acceleration = 0)...
F1+F2+F3+F4=ma=0 where F3 = (250kg*g), F4=(56.5kg*g)
F1+F2+306.5g=0

...

You're writing it in terms of g? Why're all the signs positive? Did you draw a force diagram?

 

[StudyBuddy]

I finally figured it out...

 

[StudyBuddy]

Yes, I just implicated g= -9.8m/s^2
Thank you both for your replies

 

[TomHart]

You're writing it in terms of g? Why're all the signs positive? Did you draw a force diagram?

Yeah, I was going to comment on that also. I prefer to define the forces in the direction that I know (or think) they will be in reality. In this problem, you can know ahead of time, based on the geometry, the direction of all of the forces. So I would have written F1 + F2 = F3 + F4.

Also, when I do torque calculations, rather than summing all of the forces to equal 0, it is easier for me to do CW = CCW, based on the direction that I defined all of the forces. But that is just my personal preference. I just like positive numbers better than negative numbers. :)