Tone L
- 72
- 7
- Homework Statement
- Graph a guassian pulse when the FWHM is approximately 1 ns
- Relevant Equations
- $$V(t) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-t^2}{2\sigma^2}}$$
Simply plugging this into software like MATLAB will present a solid guassian distrubution. However, my doubt comes from selecting the correct sigma.
t = - 10 ns to + 10 ns
##\sigma## = 0.1 ns
This produces a plot like so,
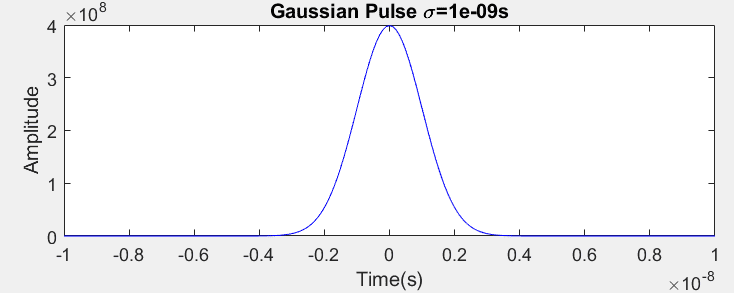
t = - 10 ns to + 10 ns
##\sigma## = 0.1 ns
This produces a plot like so,
Last edited: