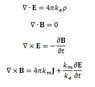The reason for the existence of ε0 and μ0 are unknown to most students, but nevertheless countless threads have been started in this forum where people looked for answers to these important, but neglected, questions. After a lot of reading, I think I came up with a good understanding of why these things exist. But I still have some questions, and I would like to ask clem to try and answer them, since he seems to know so much about this subject.
- Coulomb formulated Coulomb's Law, which gives the force between to charges under certain conditions, and goes F = ke q²/r², where ke is a constant.
- Ampère formulated Ampère's Force Law, which gives the force between two wires under certain conditions, and goes 2 km i1i2/r, where km is a constant.
- If one arbitrarily defines ke, then one is automatically defining a charge unit which makes Coulomb's Law true. Therefore, since the unit of charge and current are related (q=it), he is also defining the unit of current, and therefore defining km. The opposite is also true: if one abritrarily defines km, then he is ultimately defining ke.
- Physicists chose to define km and derive ke from km.
- First question: why did physicists choose to define km instead of ke? I read somewhere that it was because they wanted to leave the unit of current practically unchanged from the one that was currently being used. Could you elaborate on this?
- After defining km, physicists derived ke from km.
- When developing Maxwell's Equations from experimental facts, one finds that the term 4π appears in the numerator of both the first and the fourth equation. Therefore, physicists found it would be useful to express ke and km as a certain number divided by 4π, so it would cancel out in Maxwell's Equations and simplify them.
- So they said ke = (a certain number)/4π and km = (another number)/4π.
- Since the values of ke, km and 4π were known, they derived the values of both these numbers, which today we call ε0 and μ0, respectively. ε0 and μ0 also have units in order to make the units in Coulomb's and Ampère's Law match.
- Second question: physicists actually defined km to be μ0/4π, but they defined ke to be 1/4πε0! Why didn't they define ke to be ε0/4π (and changed the value of ε0, of course)? I have asked this question here before, but I want to see your take on it.
Thank you, and sorry for the madness.