drjohn15
- 13
- 0
Homework Statement
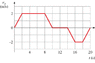
You are consulting for an elevator company. During a safety test, technicians created the following graph of the velocity of the elevator versus time; you have been asked to interpret the graph. Unfortunately, you are told that the technician who printed the graph has made two mistakes. The labeled interval on the velocity axis should be 2.1 m/s rather than 2.0 m/s, and the labeled time interval should be 4.2 s rather than 4.0 s. You should begin by redrawing the graph on your own paper with the proper labels on the velocity and time axes.
Since this motion is purely one-dimensional, give your answers to the following questions using a coordinate system consisting of a y-axis in the Up-Down direction with Up as positive. Indicate directions by the appropriate plus or minus sign. Assume that the test begins (at time zero) with the elevator at position y0=-3.1 m (i.e. 3.1 meters below ground level -- ground level has been selected as the location at which y=0).
Homework Equations
Velocity vs Time:
##t = 0\ s##, ##v = 0\ m/s##
##t = 2.1\ s##, ##v = 2.1\ m/s##
##t = 4.2\ s##, ##v = 2.1\ m/s##
##t = 6.3\ s##, ##v = 2.1\ m/s##
##t = 8.4\ s##, ##v = 2.1\ m/s##
##t = 10.5\ s##, ##v = 0\ m/s##
##t = 12.6\ s##, ##v = 0\ m/s##
##t = 14.7\ s##, ##v = 0\ m/s##
##t = 16.8\ s##, ##v = -2.1\ m/s##
##t = 18.9\ s##, ##v = -2.1\ m/s##
##t = 21\ s##, ##v = 0\ m/s##
##v = Δy/Δt## (y is the variable in this case)
The Attempt at a Solution
What is the position of the elevator at time 2.1 seconds? ... 8.4 seconds? ... etc.
##v = 2.1\ m/s = \frac{y_f - (-3.1\ m)}{2.1\ s - 0\ s}##
##\Delta y = 4.41\ m = y_f + 3.1\ m##
##y_f = 1.31\ m##
This answer is incorrect and I'm not sure where I'm going wrong with this. I even tried to enter
##1.3\ m## and that was incorrect as well.
Any help would be greatly appreciated.
Last edited: