Possibly misteaching Circuits

[DaTario]

Hi All,

Consider a circuit with two loops like the figure bellow, where V1 and V2 have different positive values:

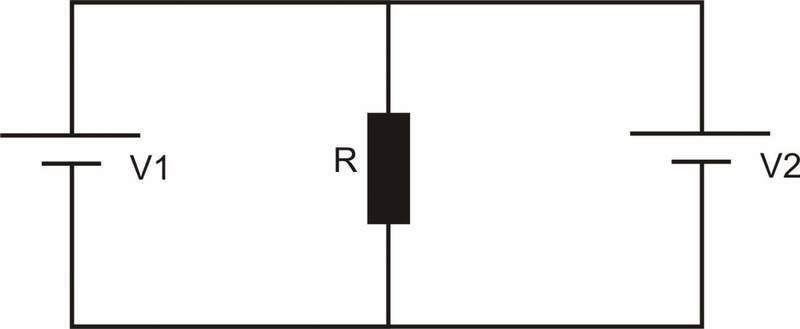
If you simply solve the equations for this circuit, you will see that the current crossing the resistance has two different values. I usually get rid of this problem by saying that we have implicitly assumed that batteries don't have internal resistance, and that this assumption is wrong. I tell my students that if you introduce even small resistances together with each battery then this non-uniqueness will disappear. My question is: is this a correct explanation of this non-uniqueness? How can one physically explain and justify this procedure, based on the kirchhoff's equations?

Thank you

Best wishes

DaTario

 

[dgOnPhys]

You cannot have ideal voltage sources in parallel (nor ideal current sources in series) because a node voltage (a branch current) has to be well defined. Your explanation is valid for a real source situation, the internal resistance will allow the calculation of the voltage across the resistive load and (assuming the voltage sources are different) you will end up with one source sinking and the other providing current... and not all voltage sources 'like' to sink current...

 

[K^2]

The assumption that wire resistances are perfectly zero is also an idealization. In a real circuit, there will be at least some resistance in the wire. Even if you somehow managed to get rid of resistance in your voltage source, you are not getting rid of resistance in the wires.

 

[Studiot]

Hello, DaTario.

Your explanation of what to do about the problem is good, so carry on using it.

However it is a getout, not a true explanation. The problem is that whilst you may well be able to appreciate the answer, students just meeting Kirchoff probably can not.

Kirchoff's laws still hold for the situation you have drawn, that is with no source series resistances.

However they have no solution.

The reason they have no solution is mathematical, not physical.
Kirchoff's laws are a bunch of simultaneous linear equations. These are not guaranteed a solution in maths and the situation you have drawn is a circuit demonstration of this. Of course your circuit cannot be realized in reality.

Consider a set of equations of the form A_nx+B_ny+C_nz = D_n. {n = 1 - 3} {A, B,C,D are constants}


This is the equation of a set of planes in x,y,z space.

The solution set corresponds to a common intersection.

Now suppose all the C's are zero ie C_n=0, (This is the situation in your circuit diagram replacing x,y and z with Kirchoff variables)

The equations become A_nx+B_ny = D_n.

Which is a set of non intersecting planes at right angles to the z axis.

This set has no solution.

 

[Dadface]

The following may be a good way to teach this:
1.Put a switch on each side of the circuit and label the voltage on each battery(eg 4V on the left and 6V on the right) and replace the resistor by a voltmeter.Tell your students that the batteries and wires have zero resistance and that the voltmeter has infinite resistance
2.Ask your students what voltage will be recorded when the left hand switch only is closed(answer=4V),then when the right hand switch only is closed(answer=6V)then when both switches are closed(answer=?)
3.This should show your students that care should be taken when using simplifying assumptions.
4.Next you could make the question more real by adding extra data ,for example the internal resistances of the batteries.Students should then get a meaningful answer to the voltage measured when both switches are closed.

 

[DaTario]

First of all Thank you All.

I would like to add what is possibly an alternative method for solving these circuits. Some students of mine, sometimes, for having already had some study on electricity before the course, bring me this method which consists in solving all the three loops as if they were isolated and, then, compute all the branch currents by adding the fictional values obtained for each branch.

If this can be done, would it be an allowed exit to the situation I presented in the OP?

Best wishes

DaTario

P.S. I have never gone into the details of this approach.

 

[Studiot]

Just how does one solve the outer loop without the resistor?

 

[DaTario]

Bingo! I guess it is it. We don't have a way to determine the current in the outer loop. So theoretically this model presents this limitation. I guess now we may say that it
is proved that this model presents this limitation.

To me the question seems to be solved now.

Thank you Studiot

Best wishes

DaTario

 

[Studiot]

I don't have time right now, but I will post a diagram about parallel generators or batteries, you might find interesting and worth leading the better students towards

 

[DaTario]

Thank you Studiot.

Best Regards,

DaTario

 

[Studiot]

OK here we are.

We have a nominal 1.5 volt battery, B₂ that is somewhat discharged to 1.4 volts and we wish to boost its performance by adding a smaller, but fresh, 1.5 cell, B₁. The diffrence in battery size is reflected in the different internal series resistances shown.

Now consider first each battery separately (that is without the other in circuit). As the current drawn by R_L increases the terminal voltage seen at AB by the load drops.

For battery B₁ it is 1.5volts at zero amps and drops at 0.2 volts per amp. This is shown as line V₁ in the diagram.

For battery B₂ it is 1.4volts at zero amps and drops at 0.1 volts per amp. This is shown as line V₂ in the diagram.

To obtain the load sharing for any given combined terminal voltage,

Draw a line parallel to the current axis ( I have shown 1.26 volts dashed) at the required terminal voltage.

Read off the intercepts I₁ & I₂ this will give the total load current = I₁ + I₂.
This gives point B on the graph.

To plot point A

Note that at zero load current there is (1.5 -1.4)/0.3 amps circulating between the batteries.
The combined terminal voltage is given by either the EMF of B₁ minus this current time O.2 ohms or the EMF of battery B₂ plus this current times 0.1 (ohms). that is 1.4333 volts.

Thus by joining points A and B you have plotted combined terminal voltage against load current.

Those with lots of times and better computer graphics resources than I possesses are welcome to construct a prettier diagram. Any copyright is waived, you are welcome to use this information in for teaching purposes.

 

[DaTario]

Note that at zero load current there is (1.5 -1.4)/0.3 amps circulating between the batteries.

I didn't get this point. Could you explain it ?

Best Regards,

DaTario

 

[Studiot]

When the load is disconnected (R_L=\infty) there is only the loop containing the two batteries and their series resistance.

Since in this loop the batteries are connected in opposition, the emf in the loop equals the difference of their EMFs ie 1.5 - 1.4 = 0.1 volts.
This EMF drives a current through the total loop resistance of (0.2 + 0.1 = 0.3) ohms.
By Ohm's law this current therefore equals 0.1/0.3 = 0.3333 amps.

If you prefer the 0.1 volts EMF in the loop is divided between the two series resistances in proportion to their values, as with any voltage divider. That is 2/3 across the 0.2 ohms and 1/3 across the 0.1 ohms.

Remember what we are talking about is the terminal voltage as seen by the outside world (ie the load resistor).

Terminal voltage = Battery EMF (which does not alter) minus the voltage drop across the internal series resistance (which depends on current drawn).

What I am showing is the effect on terminal voltage of combining two (or more) batteries in parallel.