Potential Difference of Split Capacitor: Understanding Charge Dis-Equilibrium

[Sefrez]

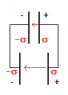
See attachment. Assume that the two capacitor's plates were originally connected together as one capacitor, and thus their plate separations were equal, along with their charge densities. In the photo below then, the capacitor has been split down the middle and with one halve the distance between the plates has been decreased. Wires are now connecting the plates.

Considering the plates were once connected, they should have equal charge densities right after the cut. This should mean that the electric field magnitude between each plate set is approximately equal - even though the plate separation differs.

Taking the potential over the two capacitors will give that the one of greater separation has greater potential. Assuming that charge density has not yet changed on any plates, the decrease in the other two plates results in a lesser potential. My question is then, why does taking potential differences imply that charge will move from the capacitor of higher potential to the one of lower potential when there seems to be no apparent forces on the charges? That is, through all this, it seems as if the charges could still be in equilibrium if the electric field between each set of plates is equal at first. I am assuming that the capacitor of greater potential difference will charge the one of less until both have equal potential differences. I just don't see where the charge dis-equilibrium comes from. It actually seems to be out of equilibrium once they are both at equal potential differences as the electric fields will now be unequal.

 

[tiny-tim]

Hi Sefrez!

Suppose you're a free'n'easy electron on the bottom left plate, looking for a good time.

You were attracted to a positive charge on the bottom right plate, but now the distance is greater, so the attraction is less.

There's zero electric field inside a conductor (in equilibrium), so you just skate over to the top left plate where all the action now is!

(until it gets too crowded because all your friends are doing the same thing! …

boy, are they repulsive sometimes! )​

 

[Sefrez]

Thanks for the reply!

Hi Sefrez!

Suppose you're a free'n'easy electron on the bottom left plate, looking for a good time.

You were attracted to a positive charge on the bottom right plate, but now the distance is greater, so the attraction is less.

There's zero electric field inside a conductor (in equilibrium), so you just skate over to the top left plate where all the action now is!

(until it gets too crowded because all your friends are doing the same thing! …

boy, are they repulsive sometimes! )​

(in bold) I can certainly see this being the case in reality, but in the case of infinite plates, wouldn't the attraction be the same regardless of distance? I know this is obviously not the case, even in the example, but it is however considered when deriving potential difference (e.g. V = ED.) So then, if the plates could be infinite giving rise to a constant E field, would there not be reallocation of charges even though the potential would be calculated to be different?

Thanks.

 

[tiny-tim]

i'm not following you

what i said applies no matter what the size or shape of the plates

 

[Sefrez]

I guess what I am saying is that the electric field between the plates would be unchanged no matter their separation. It would be something like σ/ε, correct?

I assume that this then does not apply on a small scale? But rather, individually it must still be proportional to the inverse square of their separation? I guess this makes sense due to the obvious fact that the attraction force between just two charges mathematically approaches infinity with decreasing distance at which the above does not account for.

I was looking to what is derived via calculus (or Gauss's Law,) on the force exerted, but I guess this only applies on the large scale as in the derivations perfect uniform charge density is assumed at which in reality is actually individual particles. Is this correct?

 

[tiny-tim]

Hi Sefrez!

(just got up :zzz:)

… the electric field between the plates would be unchanged no matter their separation. It would be something like σ/ε, correct?

yup, the D field is defined as σ, and then the E field is D divided by the local ε, which may be different for different dielectric in series

(this only works in series, not if the dielectrics are in parallel, because in parallel, σ is not uniform over the plate)

I assume that this then does not apply on a small scale? But rather, individually it must still be proportional to the inverse square of their separation? I guess this makes sense due to the obvious fact that the attraction force between just two charges mathematically approaches infinity with decreasing distance at which the above does not account for.

no

the electric field from a point ~ 1/r²

the electric field from a line ~ 1/r

the electric field from a plane ~ 1​

you can get all these from Gauss' law

(or from just looking at how the field lines diverge … which for a plane, they obviously don't! )

I was looking to what is derived via calculus (or Gauss's Law,) on the force exerted, but I guess this only applies on the large scale as in the derivations perfect uniform charge density is assumed at which in reality is actually individual particles. Is this correct?

no, it applies on the small scale too

it only fails to apply on the very small scale, in the gaps between adjacent charges

 

[Sefrez]

Hello. Thanks for the reply.

no

the electric field from a point ~ 1/r²

the electric field from a line ~ 1/r

the electric field from a plane ~ 1​

you can get all these from Gauss' law

(or from just looking at how the field lines diverge … which for a plane, they obviously don't! )

If this is the case, then how does the force change on the electrons as the distance increases being that the electric field is constant?

no, it applies on the small scale too

it only fails to apply on the very small scale, in the gaps between adjacent charges

Assuming that the charges lie on the surfaces, if the plates can be brought together with no lower limit (separation can be infinitely small) then there has to be some 1/r^2 > σ/ε. As r is the separation, 1/r^2 would approach infinity. So I don't see how it only fails in gaps of adjacent charges?

Thanks!

 

[sophiecentaur]

Considering the plates were once connected, they should have equal charge densities right after the cut. This should mean that the electric field magnitude between each plate set is approximately equal - even though the plate separation differs.

This is your problem. It is the Potential Differences that are equal. The Field is Potential / distance so the Field is less between the wider separated plates.
Any conclusions you have drawn from your original statement are suspect. You need to start again with your reasoning, I think.