Potential Energy and Equilibrium Position for a Circular Trajectory

[Lone Wolf]

Homework Statement

A particle of mass M = 1 kg is subject to a force F with associated potential energy U(x, y) = x^2 + y^2 (x and y in m).
a) Find F(x, y)
b) Find the equilibrium position
c) Suppose the particle has a circular trajectory around the origin. Find the radius when the total energy is 2 J.

Relevant Equations

F = - grad U

a)

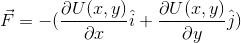
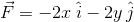
Solution given: F = - x î - y j
b)
The equilibrium position happens when F = 0.

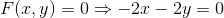
x = 0 and y = 0 is the point of equilibrium.
Solution given: (0, 0)
c)
Since the particle has a circular trajectory the trajectory equation becomes x^2 + y^2 = R^2.

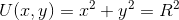
The maximum potential energy the system can achieve is 2 J (= total energy).

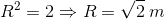
Solution given: R = 1 m

Any help is appreciated.

 

[Orodruin]

Solution given: F = - x î - y j

This is wrong.

The maximum potential energy the system can achieve is 2 J (= total energy).

This is not correct. If the trajectory is circular, the kinetic and potential energies are constant and both are non-zero.

 

[vela]

The equilibrium position happens when F = 0.
View attachment 241098

This is wrong. Force is a vector. You're treating it like a scalar.