Potential of a non-conducting sphere

[NicolaiTheDane]

UPDATE: the first 2 assignments are done (i think). I'm stuck on 3. and I have explained in attempted solution what I have tried thus far.

I have an important homework assignment due in Electromagnetism, and I have no idea where to start. It has many sub-assignments, but I cannot even figure out where to begin with the first one.

1. Homework Statement
The electrostatic potential with in a non-conducting sphere, with radius R ($r = \sqrt{x^2+y^2+z^2} < R$) is given as:

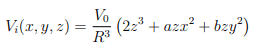
where a and b are constants, and with the origin set in the center of the sphere. The sphere has a surface charge of $\sigma$, there are no charges inside or outside the sphere, and there are no external fields. The potential has rotational symmetry around the z axis, both inside and outside, and goes to zero when $r \rightarrow \infty$.

1. (done) Find $a$ and $b$
2. (done) Express $V_i$ in $r$ and the polar angle $\theta$ around the $z$-axis, and show, that the $\theta$ dependence is given by a Legendrepolynomium $P_n(cos(\theta))$
   
3. Argue briefly, that the potentiale outside the sphere, can be written as $V_u(x,y,z)=\sum_{n=0}^\infty B_m*r^{-m-1}*P_3(\cos(\theta))$
4. Determine $B_m$ by exploiting the continuity of the potential across the sphere
5. Show that the surface charge on the sphere is $\sigma(\theta)=K*(5*\cos(\theta)^3-3*\cos(\theta)) and determine$K##

Homework Equations

No idea

The Attempt at a Solution

I haven't really a attempted a solution, as i have no idea where to start. I have considered that there might be a boundary or something that I could use, but from my reading of the book, I cannot make out what it would be (sometimes it says there are no boundary on potentials, and others times there are. Cannot differentiate between the cases). I also contemplated whether it wants me to solve the laplacian equation $\nabla^2 \cdot V=0$, but since I already have the equation, that doesn't seem to be the way to go.

EDIT: After thinking on it a bit more; If there is rotational symmetry on around the z axis, doesn't that mean that $a = b$, considering they are just constants that either increase or decrease the potential in either x or y direction? And in that case, wouldn't it be right to then take the laplacian equation $\nabla^2 \cdot V=0$, as there isn't any charges inside the sphere?

UPDATE:

Using the general solution laplace equation in spherical coordinates, for the 3. assignment $V_u(x,y,z)=\sum_{n=0}^\infty A_m*r^m+B_m*r^{-m-1}*P_3(\cos(\theta))$ I argue that $A_m=0$ as the boundary $V \rightarrow 0$ when $r \rightarrow \infty$ wouldn't be met otherwise. But beyond that I'm stuck. I don't see how I can argue the sign change in the $r$ power.

 

[Charles Link]

Your conclusion that $a=b$ is correct. When you take $\nabla \cdot E =0$ after finding $E=-\nabla V$, the solution is surprisingly simple. (And yes, that means $-\nabla^2 V=0$).

 

[NicolaiTheDane]

Your conclusion that $a=b$ is correct. When you take $\nabla \cdot E =0$ after finding $E=-\nabla V$, the solution is surprisingly simple. (And yes, that means $-\nabla^2 V=0$).

Not sure why you put a minus infront in $-\nabla^2 V=0$. My book merely states it as $\nabla^2 V=0$. But I got the answer to a simple $a=-3$

The next sub-assignment is:

• Express $V_i$ in $r$ and the polar angle $\theta$ around the $z$-axis, and show, that the $\theta$ dependence is given by a Legendrepolynomium $P_n(cos(\theta))$

This seems strange, as Legendrepolynomium is only superficially covered in the book, and I haven't ever seen them before. I'm thinking I have to do something with cylindrical coordinates, as that would be make sense with symmetry along the $z$-axis, but any pointers would be much appreciated.

EDIT: Rubbish, I express the coordinates in sphericals, and substitute for legendrepolynomials. Still don't understand how they work, but I seem to come out with something neat.

 

[Charles Link]

The minus in front of $\nabla^2 V=0$ wasn't necessary, but if there was a charge density $\rho$, the equation would read $-\nabla^2 V=\frac{\rho}{\epsilon_o}$. $\\$ I will need to look at this next part later. Today I'm a little busy for the next hour or two.

 

[NicolaiTheDane]

The minus in front of $\nabla^2 V=0$ wasn't necessary, but if there was a charge density $\rho$, the equation would read $-\nabla^2 V=\frac{\rho}{\epsilon_o}$. $\\$ I will need to look at this next part later. Today I'm a little busy for the next hour or two.

Not a problem. I'll keep working out what I can. Cheers :)

 

[Charles Link]

Just one quick comment: It will be a Legendre solution in spherical coordinates rather than cylindrical that you need to work with. Suggestion is to google that, or even try looking at older Physics Forums posts by doing a search.

 

[NicolaiTheDane]

Just one quick comment: It will be a Legendre solution in spherical coordinates rather than cylindrical that you need to work with. Suggestion is to google that, or even try looking at older Physics Forums posts by doing a search.

Yea I figured after fiddling with it. Having reduced the earlier, after inserting $a=-3$, I get:

$$V_i(x,y,z)=\frac{3*V_0}{R^3}*z*\left(\frac{2}{3}*z^2+x^2+y^2\right)$$

Substituting x,y and z, expressed in spherical coords I get

$$V_i(x,y,z)=\frac{3*V_0}{R^3}*(r*\cos(\theta))*\left(\frac{2}{3}*(r*\cos(\theta))^2+(r*\sin(\theta)*\cos(\phi))^2+(r*\sin(\theta)*\sin(\phi))^2\right)$$

Reducing that horribly mess I get:

$$V_i(x,y,z)=\frac{V_0}{R^3}*r^3*\left(5*\cos(\theta)^3-3*\cos(\theta)\right)$$

On a list of legendrepolynomials I see that $P_3(x)=\frac{5*x^3-3*x}{2} \Rightarrow 2*P_3(x)=5*x^3-3*x$

Thus I conclude that the dependence on $\theta$ can be expressed by the 2 times the 3rd legendre polynomial, and the equation does becomes:

$$V_i(x,y,z)=\frac{2*V_0}{R^3}*r^3*P_3(\cos(\theta))$$

 

[Charles Link]

On part 3, one important part of these Legendre solutions, is that for a layer of surface charge, the electric field remains finite, so that the potential must be continuous across the layer of surface charge. That would make the $\theta$ dependence of $V_{out}$ what it is, if I'm not mistaken.

 

[NicolaiTheDane]

On part 3, one important part of these Legendre solutions, is that for a layer of surface charge, the electric field remains finite, so that the potential must be continuous across the layer of surface charge. That would make the $\theta$ dependence of $V_{out}$ what it is, if I'm not mistaken.

I'm not sure I follow?

 

[Charles Link]

I'm not sure I follow?

Since the potential has $\Delta V=-\int E \cdot ds$ , in going an infinitesimal distance across a layer of surface charge, from one side to the other, since $E$ remains finite, ($E=\frac{\sigma}{2 \epsilon_o}$ from the adjacent layer of surface charge plus any additional $E$ that may result, in any case $E$ is finite), with $\Delta s$ infinitesimal, (so that $E \cdot \Delta s=0$ ), we must have $V_{out}(R, \theta)=V_{in} (R, \theta)$.

 

[NicolaiTheDane]

Since the potential has $\Delta V=-\int E \cdot ds$ , in going an infinitesimal distance across a layer of surface charge, from one side to the other, since $E$ remains finite, ($E=\frac{\sigma}{2 \epsilon_o}$ from the adjacent layer of surface charge plus any additional $E$ that may result, in any case $E$ is finite), with $\Delta s$ infinitesimal, (so that $E \cdot \Delta s=0$ ), we must have $V_{out}(R, \theta)=V_{in} (R, \theta)$.

Oh right! I thought that I was suppose to be able to figure it out without that, considering that assignment 4. requires me to specifically use that, to determine B. I'll see what happens, though I might not be able to figure out until tomorrow its getting late. Bu thanks for all your help thus far, and I hope i can camp you a bit tomorrow aswell!

 

[Charles Link]

For part 4, I think the $m=0$ term is the only one you need, but I don't have a good reason yet to justify this. If this is indeed the case, the remainder of the problem is relatively straightforward. If it does involve additional values of $m$ then it gets a little more complicated. $\\$ Assuming the net charge on the sphere is non-zero, it will necessarily have an inverse square fall-off for large $r$ in the electric field, accounting for this $\frac{1}{r}$ term in the potential. I can not presently rule out other values on $m$ also coming into play though.

 

[NicolaiTheDane]

For part 4, I think the $m=0$ term is the only one you need, but I don't have a good reason yet to justify this. If this is indeed the case, the remainder of the problem is relatively straightforward. If it does involve additional values of $m$ then it gets a little more complicated. $\\$ Assuming the net charge on the sphere is non-zero, it will necessarily have an inverse square fall-off for large $r$ in the electric field, accounting for this $\frac{1}{r}$ term in the potential. I can not presently rule out other values on $m$ also coming into play though.

EDIT: There is a mistake in my update. The $r$ in the sum part, is suppose to look like this $r^{-m+1}$, but the form I'm looking for looks like $r^{-m-1}$. I cannot edit the original post anymore, so I cannot change it unfortunately.

I'm still stuck in 3. unfortunately. Setting $V_i(R,\theta)=V_u(R,\theta)$ I stuck with this rather horrible expression:

$$\frac{2*V_0}{R^3}*R^3*P_3(\cos(\theta))=\sum_{m=0}^\infty B_m*R^{-m+1}*P_m(\cos(\theta))$$

I don't see how that'll help me much, as the only thing I needed to show 3. was to explain how the $r^{-m+1}$ ended up being $r^{-m-1}.$ (since that's the only difference between what I casually found, and what I'm suppose to show)

 

[Charles Link]

That's the general Legendre solution. That is ok. What I think this problem may ultimately require, (perhaps there is a shortcut), is to assume $m=0$ is the only term that matters, compute $B_o$, and then compute $\sigma(\theta)$. What may then be necessary to show these solutions for $V_{out}$ and $\sigma$ are correct is to compute $V_{in}$ and $V_{out}$ from $\sigma$. Perhaps there is a shortcut here in showing the $m=0$ is the only non-zero $B_m$. $\\$ And perhaps this assumption that $m=0$ is the only term in $V_{out}$ is completely wrong.

 

[NicolaiTheDane]

That's the general Legendre solution. That is ok. What I think this problem may ultimately require, (perhaps there is a shortcut), is to assume $m=0$ is the only term that matters, compute $B_o$, and then compute $\sigma(\theta)$. What may then be necessary to show these solutions for $V_{out}$ and $\sigma$ are correct is to compute $V_{in}$ and $V_{out}$ from $\sigma$. Perhaps there is a shortcut here in showing the $m=0$ is the only non-zero $B_m$. $\\$ And perhaps this assumption that $m=0$ is the only term in $V_{out}$ is completely wrong.

Oh my godness I wrote $n$ in the sum. Its suppose to be $m$. My bad. Does that change anything?

Also again. In assignment 3. I'm suppose to show, that the potential outside can be written as:

$V_o=\sum_{m=0}^\infty B_m*R^{-m-1}*P_3(\cos(\theta))$

I can get to the point where it looks like this:

$V_o=\sum_{m=0}^\infty B_m*R^{-m+1}*P_3(\cos(\theta))$

The $1$ in the $r$ have a different sign, and I'm stuck on why. Also wouldn't $m=3$ for the legendre polynomials to match up?

 

[Charles Link]

Oh my godness I wrote $n$ in the sum. Its suppose to be $m$. My bad. Does that change anything?

No, that was an obvious typo. But I just computed it: I think the total charge on the sphere is zero, which might negate the $m=0$ solution. I'm still working on it.

 

[NicolaiTheDane]

No, that was an obvious typo. But I just computed it: I think the total charge on the sphere is zero, which might negate the $m=0$ solution. I'm still working on it.

I added something else in that post, in case it hadn't updated by the time you saw it. Also the charge on the surface, is specifically said to be $\sigma$. Doesn't the exclude 0 as an option?

 

[Charles Link]

But when you compute $\int\limits_{0}^{\pi} P_3(cos{\theta}) \sin{\theta} \, d \theta$ which is proportional to $Q_{total}$ you get zero. That would indicate there won't be an $m=0$ term, and there might simply be an $m=1$ term. That's at least how it appears to me right now. And you edited it incorrectly I believe. It needs to be $r$ instead of $R$, but please get the exponents with the $m$ correct, because I'm working with your solution. (I don't have these forms memorized). In any case I think the potential outside is likely to look like $V_{out}=\frac{B}{r^2} P_3(\cos{\theta})$. I think any $\frac{B}{r}$ term is zero because the total charge is zero. $\\$ Note: If you have a non-zero total charge, then $E$ must fall off as inverse square at very large $r$, but if the net charge is zero, it normally falls off as $\frac{1}{r^3}$.

 

[NicolaiTheDane]

But when you compute $\int\limits_{0}^{\pi} P_3(cos{\theta}) \sin{\theta} \, d \theta$ which is proportional to $Q_{total}$ you get zero. That would indicate there won't be an $m=0$ term, and there might simply be an $m=1$ term. That's at least how it appears to me right now. And you edited it incorrectly I believe. It needs to be $r$ instead of $R$, but please get the exponents with the $m$ correct, because I'm working with your solution. (I don't have these forms memorized). In any case I think the potential outside is likely to look like $V_{out}=\frac{B}{r^2} P_3(\cos{\theta})$. I think any $\frac{B}{r}$ term is zero because the total charge is zero. $\\$ Note: If you have a non-zero total charge, then $E$ must fall off as inverse square at very large $r$, but if the net charge is zero, it normally falls off as $\frac{1}{r^3}$.

yea I know I screwed up with the notation. Unfortunately I cannot edit the first post anymore. Anything should be right in my later post. As for your solution, that is for assignment 4. I'm still stuck on the power change in 3. as there doesn't seem to be any good reason for it. I have asked my professor over mail, if its a mistake. Also doesn't the legendre polynomials have to be the same, both on the outside and inside?

Nevermind! The power sign is just me forgetting that $\frac{1}{r^{m+1}} = r^{-m-1}$

 

[Charles Link]

yea I know I screwed up with the notation. Unfortunately I cannot edit the first post anymore. Anything should be right in my later post. As for your solution, that is for assignment 4. I'm still stuck on the power change in 3. as there doesn't seem to be any good reason for it. I have asked my professor over mail, if its a mistake. Also doesn't the legendre polynomials have to be the same, both on the outside and inside?

Inside, the exponents of $r$ are zero and positive, because the potential must remain finite at $r=0$. Outside, the exponents must be negative, because the potential needs to go to zero as $r \rightarrow \infty$. The $\theta$ dependence will be the same for both.

 

[NicolaiTheDane]

Inside, the exponents of $r$ are zero and positive, because the potential must remain finite at $r=0$. Outside, the exponents must be negative, because the potential needs to go to zero as $r \rightarrow \infty$. The $\theta$ dependence will be the same for both.

I figured it out. It was me being silly and mixing things up. $\frac{1}{r^{m+1}} = r^{-m-1}$ which means I had the answer all along. I'll try to reread everything you wrote, and try to solve 4. I'll let you know what I find

 

[Charles Link]

Here, equation (14) is the answer I needed. $l=3$ in our solution. http://dslavsk.sites.luc.edu/courses/phys301/classnotes/laplacesequation.pdf $\\$ It is very important to have the correct form of the possible solutions. $\\$ It does appear that once $\sigma$ is computed from $V_{out}$ and $V_{in}$, i.e. from the difference in the electric fields at $r=R$, the solution will be the correct one, and doesn't require further tests to verify it.

 

[NicolaiTheDane]

Here, equation (14) is the answer I needed. $l=3$ in our solution. http://dslavsk.sites.luc.edu/courses/phys301/classnotes/laplacesequation.pdf $\\$ It is very important to have the correct form of the possible solutions. $\\$ It does appear that once $\sigma$ is computed from $V_{out}$ and $V_{in}$, i.e. from the difference in the electric fields at $r=R$, the solution will be the correct one, and doesn't require further tests to verify it.

Alright so doing assignment 4. I get the following:

When $r=R$ then $V_o=V_i$ which gives me:

$$\sum_{l=0}^\infty (B_l*r^{-l-1}*P_l(\cos(\theta))=\frac{2*V_0*R^3}{R^3}*P_3(\cos(\theta))$$

Concluding by reasoning that for the continuity to hold, and look at the general solution for both outside and inside, l = 3, because we know $V_i$'s general form has l = 3. This gets me this:

$$B_3*\frac{1}{R^4}*P_3(\cos(\theta))=\frac{2*V_0*R^3}{R^3}*P_3(\cos(\theta)) \Rightarrow B_3 = B_l = 2*V_0*R^4$$

Does that seem reasonable?

 

[Charles Link]

The next step is to calculate the electric field $E$ at $r=R$ on both sides of the surface charge, from which you can immediately compute the surface charge density $\sigma$. $\\$ Additional comment: And apparently, there is no reason to need to verify that this $\sigma$ is the correct one, by computing $V_{in}$ and $V_{out}$ from it, and making sure the results agree. The reason why it is unnecessary still eludes me presently, but perhaps you can explain why this $\sigma$ that is computed from $V_{in}$ and $V_{out}$ necessarily is the correct one.

 

[Charles Link]

Please see my additional comment in post 24.

 

[NicolaiTheDane]

The next step is to calculate the electric field $E$ at $r=R$ on both sides of the surface charge, from which you can immediately compute the surface charge density $\sigma$. $\\$ Additional comment: And apparently, there is no reason to need to verify that this $\sigma$ is the correct one, by computing $V_{in}$ and $V_{out}$ from it, and making sure the results agree. The reason why it is unnecessary still eludes me presently, but perhaps you can explain why this $\sigma$ that is computed from $V_{in}$ and $V_{out}$ necessarily is the correct one.

I ended doing the following. (Ignore the danish)

Here I argue that due to the boundary conditions across the surface, I get the equation at the bottom.

Using the following equations already found ($V_u$ found by substituting in the term found for B, into the general solution from assignment 3.)

$$V_i = \frac{2*V_0*r^3}{R^3}*P_3(\cos(\theta))$$
$$V_u = \frac{2*V_0*R^4}{r^4}*P_3(\cos(\theta))$$

Taking the derivative of both equations:

Then setting $r=R$, as we are on the sphere and solving for $\epsilon_0$ gives:

$$\sigma(\theta)=\frac{14*V_0*\epsilon_0}{R}*P_3(\cos(\theta))$$

Rewriting the legendre polynomial to figure out $K$ yields the following:

$$\sigma(\theta)=\frac{7*V_0*\epsilon_0}{R}*(5*\cos(\theta)^3-3*\cos(\theta)))$$

From this I conclude that $K=\frac{7*V_0*\epsilon_0}{R}$

 

[Charles Link]

Very good. From first looking at it, it looked like one of those that was going to be very difficult to solve, but I think you got it correct !

 

[NicolaiTheDane]

Very good. From first looking at it, it looked like one of those that was going to be very difficult to solve, but I think you got it correct !

I hope so! :) Anyway there is one last assignment.

• Determine the electrostatic energy of the system. It can be advantageous to use the relation $\int_{-1}^{1} P_m(x)^2 \, dx = \frac{2}{2 \cdot m +1}$

My solution is as follows:

I find the potential on the sphere itself. I simply use either $V_i$ or $V_u$ and let $r=R$ to get

$$V=2*V_0*P_3(\cos(\theta))$$

Then I use the equation for energy which goes like this $W=\frac{1}{2} \cdot \int_{surface} \sigma \cdot V \, da$ Plugging in $V$ and $\sigma$ I get:
\begin{align*}

W&= \frac{1}{2} \cdot \int_{surface} \frac{14*V_0 \cdot \epsilon_0}{R} \cdot P_3(\cos(\theta)) \cdot 2 \cdot V_0 \cdot P_3(\cos(\theta)) \, da \\
&= \frac{14*V_0^2 \cdot \epsilon_0}{R} \cdot \int_{surface} (P_3(\cos(\theta)))^2 \, da \\
&= \frac{14*V_0^2 \cdot \epsilon_0}{R} \cdot \int_{0}^{2 \cdot \pi} \int_{0}^\pi (P_3(\cos(\theta)))^2 \cdot r^2 \cdot \sin(\theta) \ d\theta \ d\phi \\
&= \frac{14*V_0^2 \cdot \epsilon_0 \cdot r^2}{R} \cdot \int_{0}^{2 \cdot \pi} \int_{-1}^{1} (P_3(x))^2 \ dx \ d\phi \\
&= \frac{14*V_0^2 \cdot \epsilon_0 \cdot r^2}{R} \cdot \int_{0}^{2 \cdot \pi} \frac{2}{2*3+1} \ d\phi \\
&= \frac{4*V_0^2 \cdot \epsilon_0 \cdot r^2}{R} \cdot 2 \cdot \pi \\
&= \frac{8*V_0^2 \cdot \epsilon_0 \cdot r^2 \cdot\pi}{R}

\end{align*}

(The integral change from 3rd to the 4th line, is one made int he book. I'm not entirely sure why its true, but letting maple do both integrals yields the same.)

Gotta remember $r=R$ so the final reduction gives the electrostatic energy:

$$W=8*V_0^2 \cdot \pi \cdot \epsilon_0 \cdot R$$

Now my book says that total energy of the system is determined as $W = \frac{1}{2} \cdot \int E^2 \ d\tau$ (just another way to calculate it), and considering that I have $V_0^2$ and $\cdot \pi \cdot \epsilon_0 \cdot R$ which would cancel with a set of those variable from the $E^2$, the result seems plausible, wouldn't you agree?

 

[Charles Link]

I haven't looked over every detail of your latest calculation yet, but it looks to be correct. Very good !

 

[NicolaiTheDane]

I haven't looked over every detail of your latest calculation yet, but it looks to be correct. Very good !

Alright! :D Thanks for all your help man!