Potential of Concentric Cylindrical Insulator and Conducting

[hashbrowns808]

Homework Statement

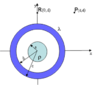
An infinitely long solid insulating cylinder of radius a = 4.3 cm is positioned with its symmetry axis along the z-axis as shown. The cylinder is uniformly charged with a charge density ρ = 28 μC/m3. Concentric with the cylinder is a cylindrical conducting shell of inner radius b = 10.1 cm, and outer radius c = 12.1 cm. The conducting shell has a linear charge density λ = -0.34μC/m.

1) What is Ey(R), the y-component of the electric field at point R, located a distance d = 48 cm from the origin along the y-axis as shown?

Homework Equations

[/B]
ρ = Q_in/V
V = 2πRL (Disregard L if I take it at 1m)
λ = Q_out/L (L @ 1m) so λ = Q
Gauss - ∫E⋅dA = Q_enclosed/∈₀
A_gauss = 2πR_a < May be area of confusion

The Attempt at a Solution

[/B]
Q_in = 2π(.043)(28x10^-6 = 7.56495X10^-6
Q_out = λ = -.34x10^-6
Q_net = 7.22495x10^-6
E = (Q_net4πk)/2πR_d
= 270935.816619 N/C

I think I might be having trouble determining where to place the outside of the Gaussian surface. I'm assuming the different fields are at:
-outside of outer conductor
-with in conductor = 0
-at inner surface of conducting shell
-between conductor and inner insulator
-surface of inner insulator
-and within the inner insulator
I think I remember seeing something different, but I'm not sure. I blasted through a similar problem last night, and somehow finished the section on Gauss' law but now I seem to have forgotten everything.

 

[BvU]

Did you already do an exercise like this but with spheres ? If you place your Gaussian surface as a cylinder around the z axis through point R, what does the theorem tell you about $\vec E$ ?

 

[kuruman]

Agauss = 2πR_a < May be area of confusion

It is indeed an area of confusion. Your expression for the area is incorrect and does not even have the correct dimensions. In fact, it is the circumference of a circle of radius R_a. You need the total area through which electric field lines emerge.

 

[BvU]

It is indeed an area of confusion. Your expression for the area is incorrect and does not even have the correct dimensions. In fact, it is the circumference of a circle of radius R_a. You need the total area through which electric field lines emerge.

I think the poster realizes that, from

Disregard L if I take it at 1m

 

[BvU]

E = (Q_net4πk)/2πR_d

I don't see this one in your relevant equations. I recognize the 2πR_d and the 4πk but I don't see a Q there, only a $\lambda$

 

[kuruman]

I think the poster realizes that, from ...

Right you are. I saw OP's earlier "V = 2πRL (Disregard L if I take it at 1m)" and I took that to be the area despite the symbol "V" defining it. I now see that this is meant as a volume, except that it's incorrect.