marino
- 9
- 1
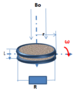
The problem: a coil of radius r, length l and N turns, rotating with constant angular velocity ω around an axis perpendicular to its simmetric axis and passing for the center of the coil. The coils is submersed in a static magnetic field, intensity B0, perpendicular to the axis of rotation of the coil. The coil is connected to a resistance R. What is the medium power dissipated by resistance?
1st solution: solving a differential equation with the current i(t) unknow I obtain:
$$-\frac{\text{d}}{\text{d}y}(B_0N\pi r^2cos(\omega t)+\frac{\mu_0 N^2 \pi r^2 i(t)}{l})=Ri(t)$$
and then the current:
$$i(t)=\frac{Rl^2 N \pi r^2\omega B_0}{((Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2)^2}sin(\omega t)-\frac{\mu_0 N^3(\pi r^2)^2 \omega^2 B_0 l}{((Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2)^2}cos(\omega t)$$
and medium power P:
$$P=\frac{R}{2} \frac{N^2 (\pi r^2)^2 \omega^2 B_0^2 l^2}{(Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2}$$
2nd solution: a virtual ca generator in series with the coil. The circuit impedance is:
$$Z=R+j\omega L$$
the Faraday-Newman-Lentz applied to the solenoid get the max fem:
$$V= N \pi r^2 \omega B_0 sin(\omega t) $$
and the current max:
$$I=\frac{V}{|Z|}$$
so, the medium power dissipated by resistance:
$$P=\frac{R}{2} I^2=\frac{R}{2} \frac{(N \pi r^2 \omega B_0)^2}{R^2+(\omega L)^2}$$
and, substituting ##L=\frac{\mu_0 N^2\pi r^2}{l}##, I obtain the same than 1st solution
3rd soultion: somewhere in internet you can find:
the Faraday-Newman-Lentz applied to the solenoid get the max fem:
$$V= N \pi r^2 \omega B_0 sin(\omega t) $$
so the max current on the resistor:
$$I=\frac{V}{R}$$
and, then the medium power:
$$P=\frac{R}{2} VI=\frac{R}{2} \frac{(N \pi r^2 \omega B_0)^2}{R^2}$$
The question:
1) have you evidence of this calculation?
2) do you know a textbook for this problem?
3) do you know a software to simulate this system (matlab, pspice, labview, ...)?
thamks!
1st solution: solving a differential equation with the current i(t) unknow I obtain:
$$-\frac{\text{d}}{\text{d}y}(B_0N\pi r^2cos(\omega t)+\frac{\mu_0 N^2 \pi r^2 i(t)}{l})=Ri(t)$$
and then the current:
$$i(t)=\frac{Rl^2 N \pi r^2\omega B_0}{((Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2)^2}sin(\omega t)-\frac{\mu_0 N^3(\pi r^2)^2 \omega^2 B_0 l}{((Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2)^2}cos(\omega t)$$
and medium power P:
$$P=\frac{R}{2} \frac{N^2 (\pi r^2)^2 \omega^2 B_0^2 l^2}{(Rl)^2+(\mu_0 N^2 \pi r^2\omega)^2}$$
2nd solution: a virtual ca generator in series with the coil. The circuit impedance is:
$$Z=R+j\omega L$$
the Faraday-Newman-Lentz applied to the solenoid get the max fem:
$$V= N \pi r^2 \omega B_0 sin(\omega t) $$
and the current max:
$$I=\frac{V}{|Z|}$$
so, the medium power dissipated by resistance:
$$P=\frac{R}{2} I^2=\frac{R}{2} \frac{(N \pi r^2 \omega B_0)^2}{R^2+(\omega L)^2}$$
and, substituting ##L=\frac{\mu_0 N^2\pi r^2}{l}##, I obtain the same than 1st solution
3rd soultion: somewhere in internet you can find:
the Faraday-Newman-Lentz applied to the solenoid get the max fem:
$$V= N \pi r^2 \omega B_0 sin(\omega t) $$
so the max current on the resistor:
$$I=\frac{V}{R}$$
and, then the medium power:
$$P=\frac{R}{2} VI=\frac{R}{2} \frac{(N \pi r^2 \omega B_0)^2}{R^2}$$
The question:
1) have you evidence of this calculation?
2) do you know a textbook for this problem?
3) do you know a software to simulate this system (matlab, pspice, labview, ...)?
thamks!
Last edited by a moderator: