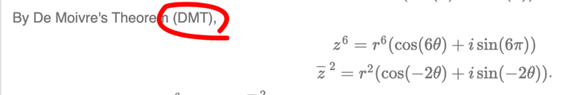- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Power of a complex conjugate
- I
- Thread starter Leo Liu
- Start date
In summary, this is true:-Euler's Formula, ##e^{i\theta}= \cos{\theta} + i\sin{\theta}##, is the most important equation in mathematics-If z=reiθ, why does z¯=re−iθ?
Mathematics news on Phys.org
- #2
- 27,243
- 18,655
If you try to justify that formula, where do you get stuck?
- #3
Leo Liu
- 353
- 156
$$\bar z^2=(x-yi)^2$$
$$\bar z^2=r^2(\cos\theta-i\sin\theta)^2$$
$$\bar z^2=r^2(\cos(2\theta)-i\sin(2\theta))$$
$$\bar z^2=r^2(\cos2\theta+i\sin(-2\theta))$$
$$\bar z^2=r^2(\cos(-2\theta)+i\sin(-2\theta))$$
I got it. Thanks.
$$\bar z^2=r^2(\cos\theta-i\sin\theta)^2$$
$$\bar z^2=r^2(\cos(2\theta)-i\sin(2\theta))$$
$$\bar z^2=r^2(\cos2\theta+i\sin(-2\theta))$$
$$\bar z^2=r^2(\cos(-2\theta)+i\sin(-2\theta))$$
I got it. Thanks.
- #4
- 27,243
- 18,655
What about:
$$\bar z^2 = (re^{-i\theta})^2 = r^2e^{-2i\theta} =r^2(\cos (-2\theta) +i\sin(-2\theta))$$
$$\bar z^2 = (re^{-i\theta})^2 = r^2e^{-2i\theta} =r^2(\cos (-2\theta) +i\sin(-2\theta))$$
- #5
Leo Liu
- 353
- 156
I actually stated that I didn't want to use this method on the course chat haha.PeroK said:What about:
$$\bar z^2 = (re^{-i\theta})^2 = r^2e^{-2i\theta} =r^2(\cos (-2\theta) +i\sin(-2\theta))$$
Thank you though! It is very neat.
- #6
FactChecker
Science Advisor
Homework Helper
Gold Member
2023 Award
- 8,530
- 4,051
You should study each part you doubt until it is intuitive to you. It is very fundamental and important.Leo Liu said:I actually stated that I didn't want to use this method on the course chat haha.
View attachment 293673
Thank you though! It is very neat.
In words explain why:
If ##z=re^{i\theta}##, why does ##\bar{z}=re^{-i\theta}##?
Then why does ##\bar{z}^2=re^{-i2\theta}##?
etc.
- #7
FactChecker
Science Advisor
Homework Helper
Gold Member
2023 Award
- 8,530
- 4,051
Many mathematicians consider Euler's Formula, ##e^{i\theta} = \cos{\theta} + i\sin{\theta}##, to be the most important equation in mathematics. You should get very comfortable with using it.
Last edited:
- #8
PAllen
Science Advisor
- 9,180
- 2,412
You can also just to algebra on the conjugate expressed in terms of ##\theta##, and then apply double angle trig formulas, if you want to see it verified brute force. It works out very straightforward this way, though, of course, using exponentials is far more elegant.
- #9
Leo Liu
- 353
- 156
I guess it's because $$\text{cis}(-\theta)=e^{-i\theta}$$.FactChecker said:If z=reiθ, why does z¯=re−iθ?
- #10
FactChecker
Science Advisor
Homework Helper
Gold Member
2023 Award
- 8,530
- 4,051
Yes. Negating the imaginary part of ##z=x+iy = r(\cos\theta+ i\sin\theta)## to get ##\bar{z}= x-iy = r(\cos\theta- i\sin\theta)## is the same as negating the argument, ##\theta##, to get ##\bar{z}=r(\cos{(-\theta)} + i\sin{(-\theta)})= r(\cos\theta- i\sin\theta)##.Leo Liu said:I guess it's because $$\text{cis}(-\theta)=e^{-i\theta}$$.
It looks like every line in your original post is correct (I didn't look hard at it.), but it is not clear how you got some lines and if you understood it. At least in the beginning, it is good practice to really spell everything out. You can skip some details after you are well beyond that level, but not before.
Last edited:
1. What is the power of a complex conjugate?
The power of a complex conjugate is a mathematical operation that involves raising a complex number to a certain exponent. It is calculated by multiplying the complex number by itself a certain number of times, as determined by the exponent.
2. How is the power of a complex conjugate different from the power of a real number?
The power of a complex conjugate is different from the power of a real number because complex numbers have both a real and imaginary component, while real numbers only have a real component. This means that the power of a complex conjugate involves both multiplication and division, while the power of a real number only involves multiplication.
3. What is the significance of the complex conjugate in the power operation?
The complex conjugate is significant in the power operation because it allows us to simplify complex numbers and make calculations easier. By multiplying a complex number by its conjugate, we can eliminate the imaginary component and end up with a real number.
4. How does the power of a complex conjugate relate to the modulus of a complex number?
The power of a complex conjugate is related to the modulus of a complex number through the formula |z|^2 = z * z*, where z* is the complex conjugate of z. This means that the modulus of a complex number is equal to the complex number multiplied by its conjugate.
5. Can the power of a complex conjugate be negative or fractional?
Yes, the power of a complex conjugate can be negative or fractional. This means that we can raise a complex number to a negative or fractional exponent, just like we can with real numbers. The resulting answer will still be a complex number.
Similar threads
-
Precalculus Mathematics Homework Help
- Replies
- 9
- Views
- 408
-
General Math
- Replies
- 20
- Views
- 2K
-
Advanced Physics Homework Help
- Replies
- 2
- Views
- 974
-
General Math
- Replies
- 3
- Views
- 2K
-
General Math
- Replies
- 5
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 5
- Views
- 571
-
General Math
- Replies
- 1
- Views
- 1K
-
General Math
- Replies
- 1
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 5
- Views
- 980
-
General Math
- Replies
- 1
- Views
- 1K
Share: