Power set (set theory) question

[Taturana]

I'm reading a book about set theory and it introduced the concept of power set. Ok, I understand what is a power set and the entire concept but I have a question about the number of elements of a power set.

There's written in the book that the number of elements of a power set is 2ⁿ where n is the number of elements of set that power set is of (very bad english, sorry). For example:

A = {1; 2; 3}

2^A = {A; {1;2}; {1;3}; {2;3}; {1}; {2}; {3}; {null set}}

n(2^A) = 2^n(A) = 2³ = 8

Using the concept of Pascal triangle we have the 2ⁿ expression comes from:

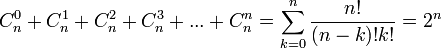
But I don't understand how can I manage this equation (before the "= 2ⁿ") to it be equals 2ⁿ

I would be grateful if someone help me...

Thank you very much

 

[statdad]

Remember that

$$(a+b)^n = \sum_{k=0}^n C^n_k a^kb^{n-k}$$

(Binomial Theorem}

Set a = b = 1; then

$$(1+1)^n = 2^n = \sum_{k=0}^n C^n_k 1^k 1^{n-k} = C^n_0 + \dots + C^n_n$$

 

[Taturana]

Thank you very much statdad for reply, you helped me a lot.

 

[HallsofIvy]

One can also prove that the power set of a set with n elements has 2ⁿ elements by induction.

The empty set, with 0 elements, has 1 subset, itself. 2⁰= 1.

Induction hypothesis: assume that, for some k, a set containing k elements has 2<sup>k[/k] subsets.

Let X be a set containing k+ 1 elements. Select one of the elements (which we can do- k+1> 0) and call it "a". All subsets of X are of two kinds, those that contain a and those that don't. Subsets of X that do not contain a are exactly the subsets of X- {a} which has k+1-1= k elements so there are 2k such subsets. Subsets of X that contain a can be written $\left{a\right}\cup U$ where U is now a subset of X that does not contain a. And, as above, there are 2k such subsets. Thus there are 2k+ 2k= 2(2k)= 2k+1[/sub] subsets of X.</sup>