Predicate logic and one point rule using Z notation

[learn_maths]

Hello all,

I'm in the process of simplifying the following equation using one-point rule and other predicate logic. But I’m a bit stuck with where to start or which inference rule to use first.

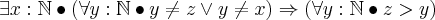
Please help or any pointers would be much appreciated.

Thanks

 

[Stephen Tashi]

learn_maths,

The notation and terminology of logic is not as standardized as the notation and terminology of a subject like Calculus. So if you ask a question about logic that uses a lot of notation, it is quite possible that people who did not study your particular textbook won't know what you're talking about.

Speaking for myself, I don't know what the "one point rule" is. I don't know what "Z notation" is. And I don't know what the \mathbb{N} means in your formula. I presume it has to do with the natural numbers, but I don't see how it relates to any of the variables.

 

[learn_maths]

Steve thanks for the reply. By far i have noticed that not many people know Z notation. And I’m quite surprised why then the universities prefer to use Z for teaching. Since I’m a learner what is the standard notation for set theory? Any links to understand the standard notation would be very helpful.

I did get same sort of reaction in few other forum when I posted Z notation.

Thanks

 

[Stephen Tashi]

I haven't opened a logic book in 30 years and I'm not current on good web sites for symbolic logic. If nobody else jumps into this thread with some recommendations, I'm sure that if you start a new thread whose title indicates you want links and books, you'll get some answers.

Do you have a good link or book for "Z notation"? I'm curious about it.

 

[learn_maths]

>Do you have a good link or book for "Z notation"? I'm curious about it.
Check this book out. The title explains what the book is all about. This is the book which I'm referring at the movement.

http://www.cs.cmu.edu/~15819/zedbook.pdf

Thanks