Pressure drop across a valve in tank

[Maximusflash]

Hey
I've gotten some good answers here before, so I'm giving it another try:
Recently I attended a building-engineering meeting, and trying to learn something new (or refresh old knowledge in some cases..) I had a hydrodynamic question/case. My firm is engineering a concrete tank for a water treatment center, so the loads on the main construction are known. But I was curious about forces on a couple of valves:

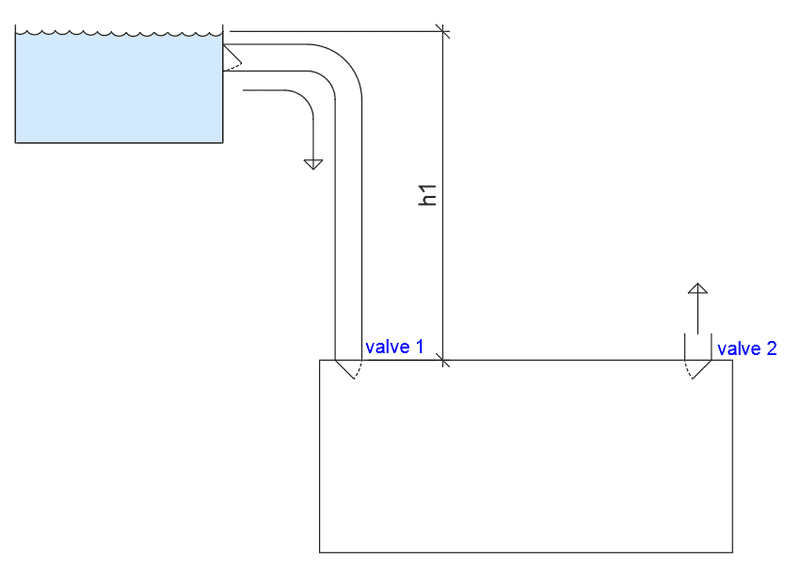
Now, the pressure in the bottom tank is given by the height from the water level into top tank, density of fluid and g. So in the case were bottom tank, top tank and tubes are full, valve 2 closed, the pressure at valve 1 would be h1 x ρ x g. This would be the case wether valve 1 is open or closed. Valve 1 would have the same pressure over it as under it, and opening/closing wouldn't change anything.
Now if everything has filled up, you close valve 1 (nothing happens). But as you open valve 2 things change. Pressure goes from h1 x ρ x g to nothing? Reference height is now equal to water height. Water will not explode out of the valve (depending on how solid the tank is: if it is elastic I guess some water could run out as it decompresses?). But at valve 1 it now has higher pressure at the top than the bottom. So we close valve 2 again, and valve 1 still has the h1 pressure at the top and nothing under. Water can not be compressed, so to even out the pressure one has to some how add pressure to the tank, or open valve 1. This will be "hard" as it has a high pressure on top of it. Could valve 1 be sort of a "spring" that compresses down to the bottom tank by the force/pressure on top of it, and equalizing the pressure before opening?

 

[mfb]

The pressure in containers fully filled with water without any open valves is problematic - if water would be perfectly incompressible and the walls would be perfect it would be ill-defined, in practice it will depend on tiny details of the setup.

You should design valve 1 to be able to handle the pressure difference.

 

[Maximusflash]

Oh, just to clarify: I am only to calculate the tank, but out of curiosity I was wondering if my initial thoughts were correct or not. So from what I see valve 1 would need to be able to withstand the h1 pressure, but when one where to open it, it would be easier to do do if the pressure some how were equal?

 

[mfb]

That depends on the design of the valve.

 

[Nidum]

With valve 1 closed tank pressure does not rise when you close valve 2 . Pressure will only rise again when you re-open valve 1 .

As @mfb suggests valve 1 could be difficult or easy to open depending on it's design . Valves though are almost always chosen to be suitable for the intended application so opening and closing valves in real plant is not normally a problem . (Assuming proper maintenance - very different story when there hasn't been any) .

Just for interest :

Ordinary tap water in a tank contains quite a lot of air and there may also be air trapped in the headspace and other voids . This air acts as a buffer making pressure in tanks relatively insensitive to minor pressurising effects . In the problem being discussed above the effect is beneficial but there are other instances where the trapped air can cause major difficulties .

An engineering company that I had done some design work for asked me one day to look at an unrelated problem which they were struggling with . They had supplied a high pressure water pump which the purchaser had intended to use for pressurising a large water filled pressure test chamber .

Everyone involved had made the usual assumption that 'water was incompressible' and that only a small amount of water would have to be pumped into raise the test chamber pressure to required level . Accordingly only a small capacity pump had been specified .

When first tried the pump took over an hour to raise the pressure - far too long for the schedule of tests
planned where pressure was to be raised and lowered several times in a day .

Reason was the air in the water . Starting from a nominally full test chamber another 2 to 3 % of chamber volume of water had to be pumped in before pressure started to rise . With a small pump and a very large chamber this took a long time .

Problem solved by installing a bleed valve and a second much larger pump to do the initial fill under more controlled conditions and to raise the pressure to a few bars above atmospheric . The smaller pump then had no difficulty taking the pressure up to the 30 to 40 bars required for tests .