Pressure Drop Testing - Too Many Unknowns?

[notapro]

Hello there,

I am having a discussion with a co-worker about a pressure drop test. I have two different 'boxes' for which I don't know the pressure drop. What I want to know is the difference in pressure drop between the two 'boxes'.

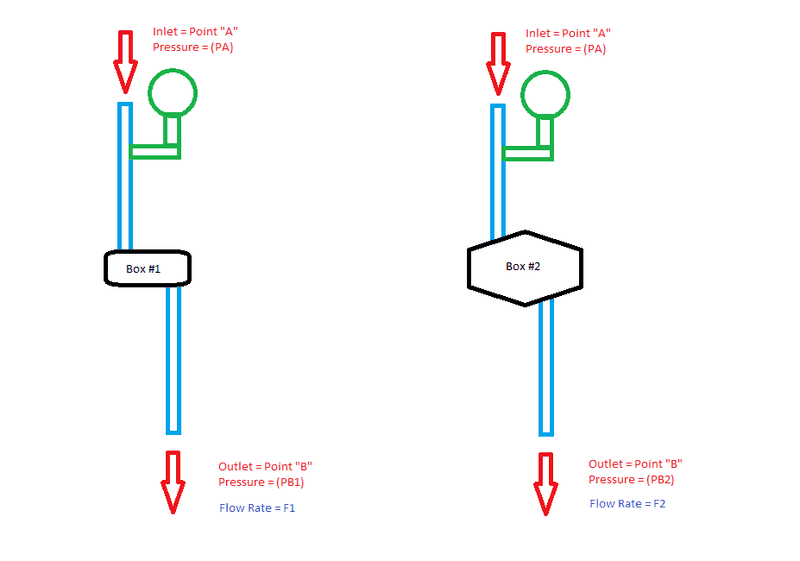
Knowns
1) P_A1 = P_A2 = P_A = Inlet Pressure for Setup 1 and 2 = Measured (Same for both setups)
2) F_A1 = F_B1 = F₁ = Flow Rate for Setup 1 = Measured (Same throughout setup 1)
3) F_A2 = F_B2 = F₂ = Flow Rate for Setup 2 = Measured (Same throughout setup 2)

Unknowns
1) P_B1 = Pressure at Outlet in Setup 1
2) P_B2 = Pressure at Outlet in Setup 2

What I want to find out
1) P_B1 - P_B2 = ΔP_B = ?

----------------------------------------------------

The first step I took is to use the equation:

\frac{F_1}{F_2} = \sqrt{\frac{P_{B1}}{P_{B2}}} (Eq. 1)

And simplified it to:

∆P_B=P_{B1}-P_{B2}=P_{B1}-P_{B1}(\frac{F_2}{F_1})^2 (Eq. 2)

So, at this point, I have two unknowns (ΔP and P_B1) and only one equation. I am claiming that we have to measure and/or solve for either P_B1 (or P_B2) in order to find an answer. My co-worker is claiming that we do NOT have to find either of these values. He wants to use another Equation 1, or something along those lines.

However, I feel you can’t use Equation 1 to compare different points in a system. For instance, Equation 3 below is NOT a usable equation.

\frac{F_{A1}}{F_{B1}} = \sqrt{\frac{P_{A1}}{P_{B1}}} (Eq. 3)

Since F_A1 = F_B1; this is meaningless, right? Or am I missing something?



Thanks in advance!
Alan

 

[mfb]

Are the boxes different, as the sketch suggests? Then it is completely impossible. You have no information about the lower part.

If the boxes are the same, all you can give is a ratio of pressure drops. Your equation 1 looks wrong, it should have the pressure drops instead of the outlet pressure. Fix it, and you get the only equation you can set up here.
It is not possible to determine the absolute pressure difference without more information. Testing the same box at different inlet pressures with constant outlet pressures would help, if measuring the outlet pressure is tricky.

 

[notapro]

Yes, they are different. I mentioned that in my second sentence; and I hoped the different shapes would illustrate that as well.

I don't understand why you think the initial equation is incorrect; when I am looking only at the outlet, I am comparing apples to apples. I guess I could change it to

\frac{F_1}{F_2} = \sqrt{\frac{P_A-P_{B1}}{P_A-P_{B2}}}

but I don't see what that would accomplish.


The reason I was only looking at the outlet is because I know they are the same, and therefore have the same K-factor, where

K=\frac{Q}{\sqrt{P}}

 

[mfb]

I don't understand why you think the initial equation is incorrect; when I am looking only at the outlet, I am comparing apples to apples.

Imagine two setups with equal inlet and outlet pressure. Flow is the same in both cases (0, assuming no pumps in the box), but the outlet pressure is different. This would violate your equation where different pressures always lead to different flow rates.

And your equation does not take into account that the boxes are different. There is absolutely nothing you can say then without more data.

I guess I could change it to

\frac{F_1}{F_2} = \sqrt{\frac{P_A-P_{B1}}{P_A-P_{B2}}}

but I don't see what that would accomplish.

It is a relation involving outlet pressures - if both boxes would be identical.

The reason I was only looking at the outlet is because I know they are the same, and therefore have the same K-factor, where

K=\frac{Q}{\sqrt{P}}

Yeah, but the boxes in the path are not...