- #1
- 3,631
- 1,511
This thought came to me while I was trying to fill my MTB bike tire a while ago as an exercise in laziness to not "check" the tire pressure with a separate gauge! Mostly, my mind just wanders...
If I have some very large tank filled with compressed air at gauge pressure Ptank. The hose runs to an idealized PRV which regulates the pressure down to Preg and holds it constant. At the other end of the hose is connected to rigid tire of volume V−tire, and initial pressure Patm (0 gauge).

How long will it take until the pressure in the tire reaches the regulated pressure ## P_{tire} = P_{reg}?
I'm just starting with Newtons Second, and analyzing from the hose to the tire and I'm already in uncharted territory:
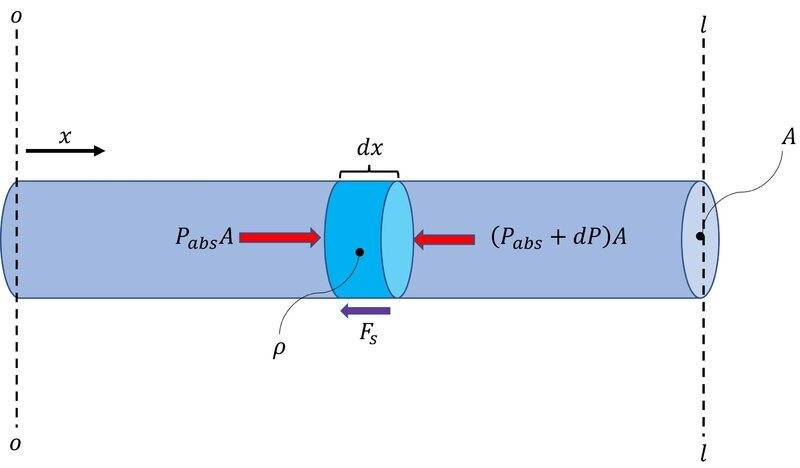
My first go was this assuming that the temperature of the flow remains constant:
$$ F_P−F_{P+dP}−F_s=A dx\frac{d}{dt} \left( \rho v \right) $$
$$ \left( P + P_{atm} \right) A - \left( P + P_{atm} + dP \right) - \tau_o \pi D dx = A dx \left( \frac{d \rho}{dt}v + \rho \frac{dv}{dt} \right) $$
Changing independent variable from time ## t ## to position along the hose ## x ##
$$ \Downarrow $$
$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{d \rho}{dx}v^2 + \rho \frac{d}{dx} \left( \frac{v^2}{2} \right) $$
The density is given from the Ideal Gas Law:
$$ \rho = \frac{P + P_{atm}}{RT} \implies \frac{d \rho}{dx} = \frac{1}{RT} \frac{dP}{dx} $$
We then have that:
$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{1}{RT} \frac{dP}{dx} v^2 + \frac{P + P_{atm}}{RT} \frac{d}{dx} \left( \frac{v^2}{2} \right) $$
Before I go any further, am I going in the right direction?
If I have some very large tank filled with compressed air at gauge pressure Ptank. The hose runs to an idealized PRV which regulates the pressure down to Preg and holds it constant. At the other end of the hose is connected to rigid tire of volume V−tire, and initial pressure Patm (0 gauge).
How long will it take until the pressure in the tire reaches the regulated pressure ## P_{tire} = P_{reg}?
I'm just starting with Newtons Second, and analyzing from the hose to the tire and I'm already in uncharted territory:
My first go was this assuming that the temperature of the flow remains constant:
$$ F_P−F_{P+dP}−F_s=A dx\frac{d}{dt} \left( \rho v \right) $$
$$ \left( P + P_{atm} \right) A - \left( P + P_{atm} + dP \right) - \tau_o \pi D dx = A dx \left( \frac{d \rho}{dt}v + \rho \frac{dv}{dt} \right) $$
Changing independent variable from time ## t ## to position along the hose ## x ##
$$ \Downarrow $$
$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{d \rho}{dx}v^2 + \rho \frac{d}{dx} \left( \frac{v^2}{2} \right) $$
The density is given from the Ideal Gas Law:
$$ \rho = \frac{P + P_{atm}}{RT} \implies \frac{d \rho}{dx} = \frac{1}{RT} \frac{dP}{dx} $$
We then have that:
$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{1}{RT} \frac{dP}{dx} v^2 + \frac{P + P_{atm}}{RT} \frac{d}{dx} \left( \frac{v^2}{2} \right) $$
Before I go any further, am I going in the right direction?