Pressure of air inside a glass

[Pushoam]

TL;DR

How does putting a cover affect the pressure inside a glass filled with air?

Let's consider an uncovered glass. Air particles are present in the glass.

$$ P_1 = P_a$$ $$P_2 =P_1 +\rho gh = P_a +\rho g h$$where $P_A$ is atmospheric pressuere and $\rho$ is air density.

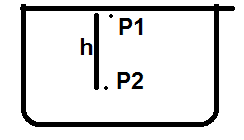
Now, if I cover the glass with a plastic card, then what is $P_1$?
$$P_2 =P_1 +\rho gh $$
1) $P_1$ is pressure due to motion of air particles and the air particles near the cover interact with the cover and its speed may change and hence $P_1$ may be less or more than $P_a$.

2) Following three forces are acting on the cover:

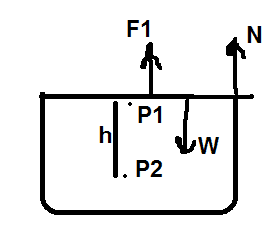
a) force due to pressure $P_1$ of air particles
b) normal force N due to glass walls
c) cover's weight W

Applying Newton's first law gives,
$$ P_1 A+ N = W$$ $$P_1 A = W - N$$
Now, since normal force is self-adjustable, let's take a light plastic card such that N = 0. Hence, in this case $P_1 A = W$.
For a plastic card with mass 20g and area 20cm², $P_1 = 10 Pa$ which is lower than the atmospheric pressure.
So, the conclusion is: putting a cover reduces the pressure of air inside the glass. Is this correct?

 

[Baluncore]

So, the conclusion is: putting a cover reduces the pressure of air inside the glass. Is this correct?

No.
There will be a hydrostatic difference in pressure due to the thickness of the card, but that difference will be overcome by the density of the card, which is resting on the glass.

 

[russ_watters]

No.
There will be a hydrostatic difference in pressure due to the thickness of the card, but that difference will be overcome by the density of the card, which is resting on the glass.

And/or the card will bend down/inward due to its own weight and the resulting pressure in the glass will be higher than atmospheric.

 

[Baluncore]

Define Pa as the atmospheric pressure at the top edge, inside the glass.
The following four forces are acting on a cover of thickness; t
a) force due to pressure of air from below; A·Pa
b) force due to pressure of air from above; A·(Pa - ρ·g·t)
c) cover's weight; W
d) normal force upwards due to glass wall; N
N + A·Pa = W + A·(Pa - ρ·g·t)
N = W - A·ρ·g·t
A·ρ·g·t is the buoyancy of the card