Pressure required for water discharge

[praveenncyr]

Hello everyone,

I am very interested in knowing the relation to determine the pressure required to push the water upstream.

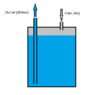
In the attached picture, water is filled inside a tank of volume V and air is constantly flowing inside the tank through an inlet with constant flow rate M. Water should be discharged with a flow rate of W through the outlet. The outlet is maintained at a pressure of P2. Now, considering the fact that air is compressible and temperature dependent, how could I calculate the pressure required by air at the top of water to push the water out through the outlet?

I am sorry for not being so specific about the dimensions. I just want to relate it somehow! Your comments are highly appreciated!

 

[russ_watters]

In US/imperial units, pressure is often expressed in height of a water column. That's your minimum required pressure here, plus your outlet pressure.

 

[BvU]

Hello @praveenncyr , !

I am sorry for not being so specific about the dimensions.

Maybe so, but it does make a difference if the water has to be pushed up 10 cm or 10 floors of a building !

https://en.wikipedia.org/wiki/Pressure#Fluid_pressure

 

[BvU]

In US/imperial units, pressure is often expressed in height of a water column. That's your minimum required pressure here, plus your outlet pressure.

Hey, that's a coincidence ! In normal units too !

 

[russ_watters]

Hey, that's a coincidence ! In normal units too !

What are "normal" units?

I've seen atmospheric pressure in mm of mercury of course, but I'm not sure I've ever done an SI pump sizing. For airflow, I always see inches of water converted to Pascals.

 

[BvU]

What are "normal" units?

After some research, I concluded the physics is independent of the system of units used to express the relationships! So, in that respect, even us/Imperial units could be considered to be somewhat normal !

But let's lure @praveenncyr to reveal to us helpers what he/she actually wants! (as opposed to discussing what we consider decent versus backward systems of units )

 

[Lnewqban]

I am sorry for not being so specific about the dimensions. I just want to relate it somehow! Your comments are highly appreciated!

Welcome!
As dimensions of the tank grow, the ability to supply enough flow of air becomes more important, if certain amount of water flow is needed.
You will also need to consider resistance to the flow of water imposed by the pipe system to which the tank could be connected to.

 

[praveenncyr]

Thanks everyone for your showing interest.

Lets discuss it with an example...The tank has a capacity of 70 litres and the water should be rised just above the tank. Let's say that the height of tank is 0.6 m and the radius of tank is 0.2 m. The diameter of air inlet and water outlet pipes are both 0.013 m. Air flows inside the tank with constant flow rate at 20°c. Now, I would like to know the pressure at inlet and outlet, considering 8E-5 m^3/s of water is being discharged.

I am in need of a relation to calculate it!

 

[BvU]

I am in need of a relation to calculate it!

Several relations !
First you have the already mentioned $\Delta p = \rho g\; \Delta h$ for the water.
For the air, use $pV = nRT$, the ideal gas law.
And you can't fix all variables you mention: for a given flow of water, the flow of air follows.

Oh, and at the outlet the water pressure is astmospheric.

 

[praveenncyr]

Several relations !
First you have the already mentioned $\Delta p = \rho g\; \Delta h$ for the water.
For the air, use $pV = nRT$, the ideal gas law.
And you can't fix all variables you mention: for a given flow of water, the flow of air follows.

Oh, and at the outlet the water pressure is astmospheric.

Thanks for your comment, I kind of need a correlation...

Yes, the pressure at outlet is atmospheric pressure.

 

[russ_watters]

...the water should be rised just above the tank.

You gave numbers for almost everything except the most important thing: we need to know how high the outlet is above the water level in the tank.

 

[praveenncyr]

You gave numbers for almost everything except the most important thing: we need to know how high the outlet is above the water level in the tank.

The outlet is 0.75 m higher from the bottom of the tank.

 

[BvU]

I am very interested in knowing the relation to determine the pressure required to push the water upstream.

So, with the tank full, you need a little more than atmospheric pressure to push some liquid out.
And with the tank as good as empty, that requires a little over 1.6 Bar
(to be precise: atmospheric + 0.6 $\rho g$ ).

In between, the relationship is linear.

Pressure drop due to friction can be ignored at such a low flowrate.

Is this somewhat clear ?

(edit: at first the tank was 0.6 m... and the outlet just above. Just above is negligible, a quarter tank height is not !)

(edit2: is this a state secret project that you are so sparse, handing out required information bit by bit after being pressed ? )

 

[russ_watters]

The outlet is 0.75 m higher from the bottom of the tank.

...we need to know how high the outlet is above the water level in the tank.

Edit: or more to the point, as the tank empties, the required pressure increases.

 

[praveenncyr]

So, with the tank full, you need a little more than atmospheric pressure to push some liquid out.
And with the tank as good as empty, that requires a little over 1.6 Bar
(to be precise: atmospheric + 0.6 $\rho g$ ).

In between, the relationship is linear.

Pressure drop due to friction can be ignored at such a low flowrate.

Is this somewhat clear ?

(edit: at first the tank was 0.6 m... and the outlet just above. Just above is negligible, a quarter tank height is not !)

(edit2: is this a state secret project that you are so sparse, handing out required information bit by bit after being pressed ? )

It is so obvious that the pressure inside the tank should be higher than the outlet pressure. Since the air is compressible, it is not necessary that the amount of air going inside would displace the same amount of water, also the space about the water level filled by air is time dependent. So, I would also like to know the flow rate of air necessary to displace the required amount of water at the outlet!

 

[praveenncyr]

...we need to know how high the outlet is above the water level in the tank.

Edit: or more to the point, as the tank empties, the required pressure increases.

It is totally time dependent, initially its 0.2 m higher than the water level. Also I don't want the specific solution value to my problem. I would like to understand the calculation procedure and the relation between them!

 

[praveenncyr]

So, with the tank full, you need a little more than atmospheric pressure to push some liquid out.
And with the tank as good as empty, that requires a little over 1.6 Bar
(to be precise: atmospheric + 0.6 $\rho g$ ).

In between, the relationship is linear.

Pressure drop due to friction can be ignored at such a low flowrate.

Is this somewhat clear ?

(edit: at first the tank was 0.6 m... and the outlet just above. Just above is negligible, a quarter tank height is not !)

(edit2: is this a state secret project that you are so sparse, handing out required information bit by bit after being pressed ? )

Ha Ha... its not a state secret project...I don't have specific values...I just want to know how to solve it!

 

[BvU]

It is so obvious that the pressure inside the tank should be higher than the outlet pressure.

Good. So you have a required pressure as a function of the liquid level.

I would like to understand the calculation procedure and the relation between them!

See #9: the ideal gas law tells you how much air is needed in the gas volume.