- #1
jkristia
- 54
- 0
The problem and my attempt at a solution is shown in the attached image.
The problem is that I end up with one extra x in the denominator.
So the question is: Is my expression for y'' correct and I just made a mistake somewhere (I have checked it several times), or am I missing something in the expression for y' and/or y'' ?
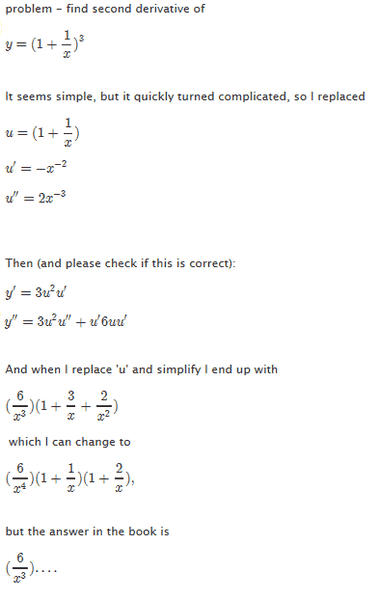
The problem is that I end up with one extra x in the denominator.
So the question is: Is my expression for y'' correct and I just made a mistake somewhere (I have checked it several times), or am I missing something in the expression for y' and/or y'' ?