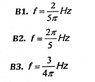Giannakoulis
- 8
- 0
Member advised to use the homework template for posts in the homework sections of PF.
In the figure below we put a small coin on a disc, which rotates at constant frequency f, at a distance D=0.2m by the disc rotation axis. If the coefficient of friction is μ=0.5, then what is is the maximum frequency that can have the disc so that the currency does not slip? g=10 m/sec^2
Anyone could help me how to start? I know that i can take Fk=Ts=m*v^2/D and replace the velocity with v=2πDf but i don't know the mass.. am i on the right way? Ts=static friction
Anyone could help me how to start? I know that i can take Fk=Ts=m*v^2/D and replace the velocity with v=2πDf but i don't know the mass.. am i on the right way? Ts=static friction
Attachments
Last edited: