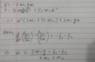Problem in getting correct coefficients of frictional forces

[Amitayas Banerjee]

I am getting correct equations on using the Lagrangian method in Systems with no non conservative forces, but when I use it in Systems with friction, sometimes I get correct equations, and sometimes I do not. Most of the equations have some problem with the coefficients of the frictional forces.
For example, let us take a look at this system...

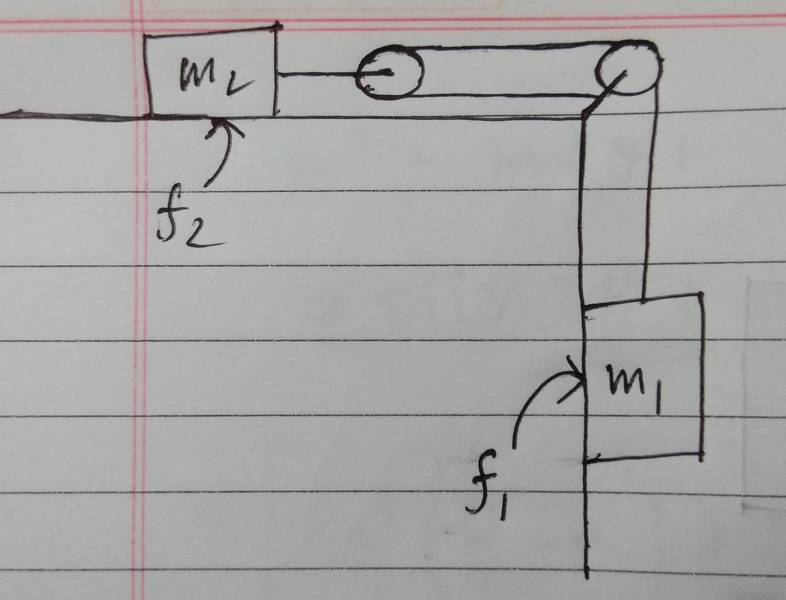
Here f1,f2 are the frictional forces(and not the coefficients of friction)

Now, let the block with mass $m_2$ move through a distance $x$ to ward the right.

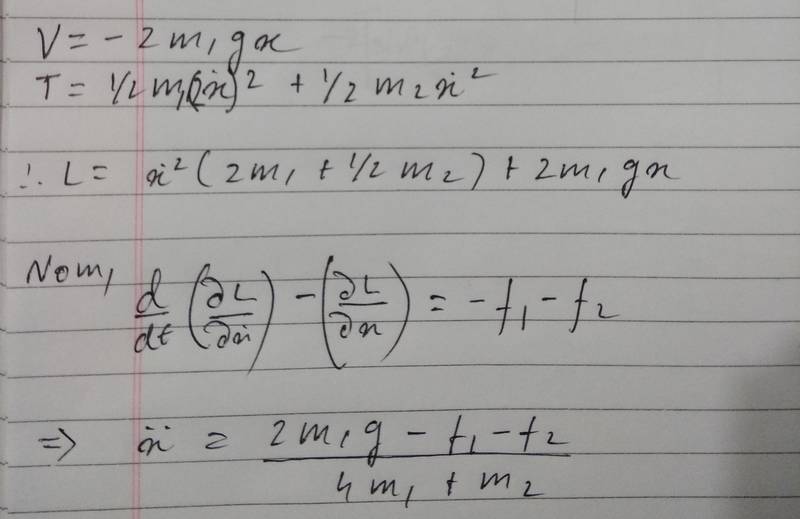
now, when we apply Newton's second law, we see that this is wrong and the coefficient of f1should have been 2
Why is the problem?...on the right hand side I have written the generalized force and the the two Lagrangian terms on the left hand side. Please help me out.

 

[Orodruin]

Standard Lagrangian mechanics does not handle dissipative systems.

 

[Amitayas Banerjee]

Standard Lagrangian mechanics does not handle dissipative systems.

I have not used that...I have used the version with generalized forces(RHS has got -f1-f2)

 

[Dale]

I have not used that...I have used the version with generalized forces(RHS has got -f1-f2)

The RHS that you wrote is not the generalized forces, it is the regular forces. The generalized forces are
$$F_i \cdot \frac{\partial v_i}{\partial \dot{q_j}}$$
That is where the factor of 2 comes in

 

[Amitayas Banerjee]

The RHS that you wrote is not the generalized forces, it is the regular forces. The generalized forces are
$$F_i \cdot \frac{\partial v_i}{\partial \dot{q_j}}$$
That is where the factor of 2 comes in

Sirl, is that vi=xdot i?

 

[Dr.D]

Standard Lagrangian mechanics does not handle dissipative systems.

I'm not sure what "standard" means in this context, but I use Lagrange frequently for systems involving losses. See Goldstein, pp. 38 - 40.

 

[Amitayas Banerjee]

Sirl, is that vi=xdot i?

@Dr.D Sir, can you clarify this?

 

[Dale]

Sirl, is that vi=xdot i?

Yes

 

[Orodruin]

I'm not sure what "standard" means in this context, but I use Lagrange frequently for systems involving losses. See Goldstein, pp. 38 - 40.

What edition are you using? Pages 38 to 40 in my Goldstein is just general variational calculus.

Anyway, I read the OP and replied a bit fast it seems. By "standard" I was meaning only letting the variation of an action be equal to zero, which is what most students learn first and many do not go beyond. For some reason I thought the OP was trying to do something like trying to introduce friction forces in the Lagrangian.

 

[Dr.D]

What edition are you using?

There is no edition number in my copy, only a 1959 copyright date and the notation 6th printing. For this reason, I presume it is a 1st edition. I used it as a textbook in the school year 1963-64. I've been using this to good effect ever since.