- #1
JohnnyGui
- 796
- 51
I was looking at the following graph showing the relationship between redshift and distance for a constant, accelerating and decelerating expansion of the universe.
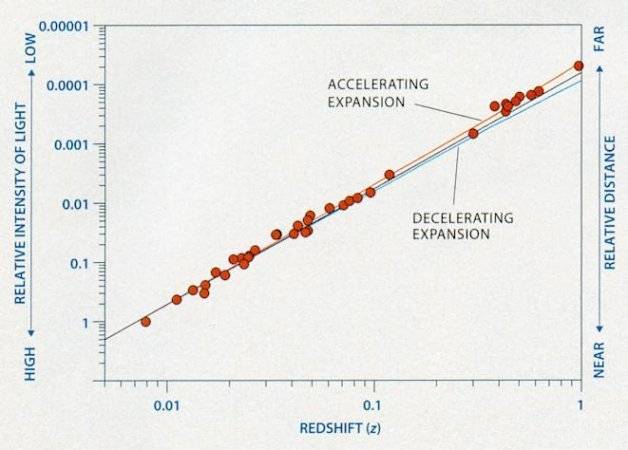
Source
Looking at the accelerating expansion line (red), I tried to reason why it would show a line that deviates upwards from the proportional one. I reasoned that it was so because, as a galaxy is further away, we would receive an older light, at the time when the galaxy was receding at a slower recession velocity than it was now. Thus, we receive the redshift based on an older (slower) velocity, meaning that redshift would not change too much as expected with a fixed increase in distance, making the line go upwards.
However, even though this reasoning gives me the expected line, when reviewing this reasoning I noticed that this is the ordinary Doppler shift which is not similar to the cosmological one. The problem is that when I reason according to the Cosmological Redshift, my conclusion tends to collide with the above graph.
My reasoning in the case of the cosmological redshift is as follows. In addition to redshift being based on the recession velocity, during the travel of emitted light towards us, its redshift would also adapt to changes in the expansion rate that occurs during that travel. Such that the redshift that we receive is representing the net result of recession velocity at the time the light was emitted + the changes in expansion rate until we received that light.
Thus, redshift of emitted light from a nearby galaxy would be based on a relatively small change in acceleration of the expansion until we receive it. In contrast, redshifted light of a very far galaxy, that is emitted a long time ago, is based on a large change in accelerated expansion rate since it was longer subject to it during its travel towards us.
Therefore, I’d conclude that light of a very far galaxy would be more redshifted than light of a nearby galaxy. And this would lead me to reason that the graph line for an accelerated expansion rate would have to deviate downwards from the proportional line since a fixed distance increase would give a larger redshift.
This reasoning does not match the accelerating graph line since it deviates upwards instead. The only explanation I could think of for this is because Cosmological Redshift is a combination of redshift based on the recession velocity + change in expansion rate, in such a way that the change in expansion rate was not sufficient to compensate for the relatively low recession velocity back at the time the light was emitted. However, this explanation would make a decelerating expansion rate show an even more upwards deviating line.
I would like to know where and why I reasoned wrong.
Source
Looking at the accelerating expansion line (red), I tried to reason why it would show a line that deviates upwards from the proportional one. I reasoned that it was so because, as a galaxy is further away, we would receive an older light, at the time when the galaxy was receding at a slower recession velocity than it was now. Thus, we receive the redshift based on an older (slower) velocity, meaning that redshift would not change too much as expected with a fixed increase in distance, making the line go upwards.
However, even though this reasoning gives me the expected line, when reviewing this reasoning I noticed that this is the ordinary Doppler shift which is not similar to the cosmological one. The problem is that when I reason according to the Cosmological Redshift, my conclusion tends to collide with the above graph.
My reasoning in the case of the cosmological redshift is as follows. In addition to redshift being based on the recession velocity, during the travel of emitted light towards us, its redshift would also adapt to changes in the expansion rate that occurs during that travel. Such that the redshift that we receive is representing the net result of recession velocity at the time the light was emitted + the changes in expansion rate until we received that light.
Thus, redshift of emitted light from a nearby galaxy would be based on a relatively small change in acceleration of the expansion until we receive it. In contrast, redshifted light of a very far galaxy, that is emitted a long time ago, is based on a large change in accelerated expansion rate since it was longer subject to it during its travel towards us.
Therefore, I’d conclude that light of a very far galaxy would be more redshifted than light of a nearby galaxy. And this would lead me to reason that the graph line for an accelerated expansion rate would have to deviate downwards from the proportional line since a fixed distance increase would give a larger redshift.
This reasoning does not match the accelerating graph line since it deviates upwards instead. The only explanation I could think of for this is because Cosmological Redshift is a combination of redshift based on the recession velocity + change in expansion rate, in such a way that the change in expansion rate was not sufficient to compensate for the relatively low recession velocity back at the time the light was emitted. However, this explanation would make a decelerating expansion rate show an even more upwards deviating line.
I would like to know where and why I reasoned wrong.
Last edited: