dpa
- 146
- 0
Hi All,
This is algebraic proof of Vandermonde's identity:
I am having some problem understanding how we reached the second last step and more importantly, last steps from revious steps.
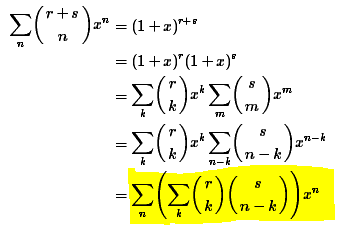
src::proofwiki.org
I would be grateful if someone would elaborate it clearly.
Basically none that are relevant to answer my question.
I have no idea how we reached the last two steps.
Thank You.
Homework Statement
This is algebraic proof of Vandermonde's identity:
I am having some problem understanding how we reached the second last step and more importantly, last steps from revious steps.
src::proofwiki.org
I would be grateful if someone would elaborate it clearly.
Homework Equations
Basically none that are relevant to answer my question.
The Attempt at a Solution
I have no idea how we reached the last two steps.
Thank You.
Attachments
Last edited: