Amaelle
- 309
- 54
- Homework Statement
- Compute the integral (3x dx dy), where the region of equation is : (x − 1)^2 + y^2 ≤ 1, 0 ≤ y ≤ x
- Relevant Equations
- 0<=r<=2cos(θ),
I already have the solution in which the region of integration has been divided into two regions
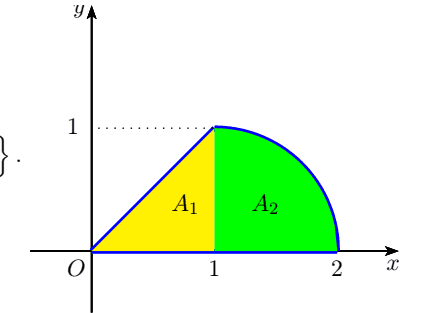
but I was wondering if I can only use one region considering the polar coordinate system) the disk equation for me is r=2cos(θ) and the theta goes from 0 to (pi/4)
0<r<2cos(θ) and the 0 <θ<pi/4
the total integral becomes
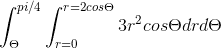
is my approach is correct?
Thanks a lot in advance!
but I was wondering if I can only use one region considering the polar coordinate system) the disk equation for me is r=2cos(θ) and the theta goes from 0 to (pi/4)
0<r<2cos(θ) and the 0 <θ<pi/4
the total integral becomes
is my approach is correct?
Thanks a lot in advance!
