Problem with f=ma and E=0.5mv^2

[Nal]

EDIT: The question has been answered, and I don't need help anymore. Thanks a lot everybody!

Hi. This is something that has been puzzling me for a while, probably just due to my own stupidity. It seems to me that this should be really simple, but I don't know what I'm doing wrong though, so now I'm putting it out here.

Imagine an object with a mass of 1 kg being accelerated at a rate of 1 m/s^2 over 10 seconds.
We can then calculate the force being applied to the object
F=1*1=1 N

We can also calculate how far the object has moved over these 10 seconds

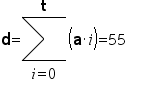
According to Wikipedia, the work (W) is the product of a force times the distance through which is acts, measured in Joules, so
W=F*d=m*a*d=55 J

The velocity v at which the object moves is t*a=10 m/s
Then we can calculate the kinetic energy E

E=0.5*m*v^2=50 J

But shouldn't E and W be the same?
For example, if we take the object, now with the kinetic energy E and make it go up a hill on a planet where the gravitational acceleration is 1 1m/s^2 (which is =a from before, of course) we will convert the kinetic energy to potential energy, and we can calculate how far up the hill the object will go, as E(kin)+E(pot) is constant

0.5*m*v^2=m*a*h
0.5*1*10^2=1*1*h
h=50 m

But shouldn't h be 55 metres, as that was the distance the object moved when we accelerated it?
I hope you understood what I meant, I'm absolutely horrible at explaining my thoughts.
Thanks in advance! :)

 

[technician]

The distance traveled is not 55m.
Check your calculation

 

[Nal]

The distance traveled is not 55m.
Check your calculation

Distance traveled over time

after 1s: 1 m (velocity 1 m/s)
2s: 3 m (velocity 2 m/s)
3s: 6 m (velocity 3 m/s)
4s: 10 m (velocity 4 m/s)
5s: 15 m (velocity 5 m/s)
6s: 21 m (velocity 6 m/s)
7s: 28 m (velocity 7 m/s)
8s: 36 m (velocity 8 m/s)
9s: 45 m (velocity 9 m/s)
10s: 55 m (velocity 10 m/s)

 

[D H]

Your calculations are incorrect. Given a constant acceleration a, distance d as a function of time is given by d=\frac 1 2 a t^2.

 

[Nal]

Ah, well that obviously solves it. Thanks a lot.

 

[azizlwl]

We can also calculate how far the object has moved over these 10 seconds

[/QUOTE

Can you elaborate more on the method you use in finding the distance?

 

[Nal]

We can also calculate how far the object has moved over these 10 seconds

[/QUOTE

Can you elaborate more on the method you use in finding the distance?

I should update the main post. I realize now that I should have used integrals to calculate the distance travelled, however I've never learned about any of that. My question has already been answered. Thanks for taking your time to reply, though!