Problem with zero net torque using a particular axis.

[DocZaius]

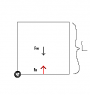
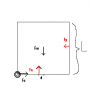
I was looking at a situation where a fridge in the back of a truck is just about to tip back due to the truck's acceleration. I am looking at the moment just before it tips. The net torque here is 0 since it is not yet tipping back. I thought I was allowed to pick any axis I wished and so picked the one where both the normal force and static frictional force were, in order to give them a zero moment arm. The reason both those forces are at that corner is that the fridge is just about to tip over and that's where the forces are acting (wrong assumption?)

Unfortunately that seems to leave me with an unphysical statement that

Net torque on fridge = 0 = mg(L/2)
where L/2 is the weight's moment arm.

What did I do wrong?

 

[Doc Al]

Unfortunately that seems to leave me with an unphysical statement that

Net torque on fridge = 0 = mg(L/2)
where L/2 is the weight's moment arm.

What did I do wrong?

You are taking moments about an accelerating reference point. In such a situation, the net torque does not equal the rate of change of angular momentum about that axis.

Essentially, when viewing things from an accelerated frame, you must add an inertial force due to the truck's acceleration. If you do, you'll find that the net torque--including that inertial force--will be zero.

 

[AlephZero]

I was looking at a situation where a fridge in the back of a truck is just about to tip back due to the truck's acceleration.

What did I do wrong?

You forgot about the words I put in bold.
The truck is accelerating, therefore it is not a Newtonian frame of reference.

The straightforward way to solve this is use F = ma in the horizontal and vertical directions. That will give you two equations for the normal force and the friction force, without getting tied in knots about what "rotation in an acclerating framce of reference" means.

The less straightforward way is to work in the accelerating reference frame by adding a fictitious force (the d'Alembert force) equal to -ma, and then take moments. I recommend sticking with the straightforward way, until you are really confident you know what you are doing.

 

[DocZaius]

You forgot about the words I put in bold.
The truck is accelerating, therefore it is not a Newtonian frame of reference.

The straightforward way to solve this is use F = ma in the horizontal and vertical directions. That will give you two equations for the normal force and the friction force, without getting tied in knots about what "rotation in an acclerating framce of reference" means.

The less straightforward way is to work in the accelerating reference frame by adding a fictitious force (the d'Alembert force) equal to -ma, and then take moments. I recommend sticking with the straightforward way, until you are really confident you know what you are doing.

Interesting, thanks. My professor was showing an example of an accelerating frame where instead of setting net horizontal force to 0 as is done in a static equilibrium problem, he set it equal to ma.

That was fine, but then he set the net torque equal to zero and tried to go about solving using the axis I have above. He got stuck on the equation I had above and then explained that if he used an axis about the center of mass of the fridge, it would be fine.

I thought one could pick any axis which led me to ask this question.

So just to be clear: It was wrong of my professor to both set net torque equal to zero and not include this fictitious force?

 

[Doc Al]

That was fine, but then he set the net torque equal to zero and tried to go about solving using the axis I have above. He got stuck on the equation I had above and then explained that if he used an axis about the center of mass of the fridge, it would be fine.

It is true that if he chose an axis about the center of mass, that the net torque would be zero. Even though the center of mass is accelerating.

I thought one could pick any axis which led me to ask this question.

Sure, if you know what you're doing. If you choose an accelerating point as your axis, it's not true that net torque equals zero.

So just to be clear: It was wrong of my professor to both set net torque equal to zero and not include this fictitious force?

Yes. That's where he messed up.

 

[nonequilibrium]

Okay, I understand that the frame of reference that was used is invalid, but I don't understand that if we're working the OP's frame the torque is non-zero: the F_n vector is drawn in the origin, but shouldn't it be in the middle of the bottom line of the fridge? And then the torque is zero. What am I seeing wrongly?

 

[AlephZero]

Okay, I understand that the frame of reference that was used is invalid, but I don't understand that if we're working the OP's frame the torque is non-zero: the F_n vector is drawn in the origin, but shouldn't it be in the middle of the bottom line of the fridge? And then the torque is zero. What am I seeing wrongly?

The OP's diagram is correct. If the box was actually tipping backwards (i.e. rotating about the back edge of the box) then only the back edge is in contact with the truck. The same is true when it is just starting to tip.

 

[nonequilibrium]

oh, like that, thank you!

 

[DocZaius]

This problem had me thinking: Does the normal force slowly wander over to the back corner as acceleration increases, or is it always at the center and then suddenly go to the back at the time tipping occurs?

Consider a square with its axis of rotation in the lower left corner and with side length = L. There is no accelerating frame (the square is not on a truck). Initially it has a net torque of 0. Weight and normal force both act with the same moment arm, same magnitude, and opposite directions.

(positive is counterclockwise)
Net torque = 0 = (normal force * (L/2)) - (weight * (L/2))

Now consider a force being applied towards the left and acting at the midpoint of the right side. If the force being applied is small, there is zero net torque. But where does the torque countering this newly applied torque come from? It can't come from static friction since that acts through the axis of rotation. The weight acts through the same point it did before so it doesn't seem to be that. All that's left is the normal force. It must move its point of action at some distance d to the left of the midpoint of the bottom side, thereby no longer perfectly countering the weight's torque.

Net torque = 0 = (force of push * (L/2)) + (normal force * ((L/2)-d)) - (weight * (L/2))

This is the only scenario that seems to account for a zero net torque: a wandering normal force. Of course as the force of the push increases, the distance "d" that the normal force acts on increases until it reaches (L/2). Then tipping occurs.

What seems weird to me is that the location of the normal force would move like that. My intuition would have me think that until there is actual rotation, a very straight cube on a very straight floor applies equal pressure at all points on the floor, but this apparently isn't the case. Thoughts (or corrections/issues)?

P.S.: I checked using other axes of rotation and the static friction acts in the bottom left throughout the entire time the pushing force increases. It does not change location with increasing pushing force as the normal force does. Also, it does not act in the center of the bottom side. Can someone give an intuitive explanation why the static force acts in the bottom left and not, say, at the point of contact of the normal force?