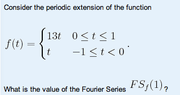SUMMARY
The discussion focuses on the convergence of Fourier Series at points of discontinuity, specifically at a point \( t_{0} \) where the function \( f(t) \) is not continuous. It establishes that the Fourier Series converges to the average of the left-hand and right-hand limits at that point, expressed mathematically as \( S_{0} = \frac{1}{2} \{\lim_{t \rightarrow t_{0} +} f(t) + \lim_{t \rightarrow t_{0} -} f(t)\} \). This conclusion is critical for understanding the behavior of Fourier Series in signal processing and mathematical analysis.
PREREQUISITES
- Understanding of Fourier Series and their properties
- Knowledge of limits and continuity in calculus
- Familiarity with mathematical notation and symbols
- Basic principles of signal processing
NEXT STEPS
- Research the implications of discontinuities in Fourier Series
- Study the Dirichlet conditions for Fourier Series convergence
- Explore applications of Fourier Series in signal reconstruction
- Learn about the Gibbs phenomenon and its effects on convergence
USEFUL FOR
Mathematicians, engineers, and students in fields such as signal processing, applied mathematics, and physics who are interested in the properties and applications of Fourier Series.