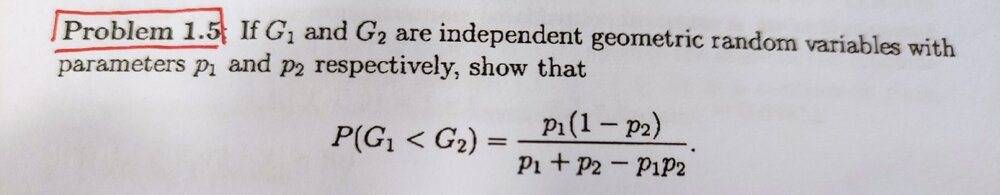Proof of a formula with two geometric random variables

[Armine]

Homework Statement

If G_1 and G_2 are independent geometric random variables with parameters p_1 and p_2 respectively, show that

Relevant Equations

P(G_1<G_2)=p_1(1-p_2)/(p_1+p_2-p_1p_2)

The image above is the problem and the image below is the solution I have tried but failed.

 

[FactChecker]

You first equation is multiple-counting many cases. You should sum the cases where $G_1 = k$, not $G_1 \le k$

 

[Armine]

You first equation is multiple-counting many cases. You should sum the cases where $G_1 = k$, not $G_1 \le k$

Get it, thank you very much!